题目内容
16.如图1,在正方形ABCD中,P是对角线BD的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.(1)求证:PC=PE;
(2)若PD=DE,求证:BP=BC;
(3)如图2把正方形ABCD改为菱形ABCD,其它条件不变,当∠ABC=120°时,连接CE,∠BAP与∠DCE有何数量关系?证明你的结论.

分析 (1)欲证明PC=PE,只要证明△ADP≌△CDP即可.
(2)只要证明∠BPC=∠BCP即可.
(3)结论:∠BAP=∠DCE,只要证明△PCE是等边三角形即可解决问题.
解答 (1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP,
在△ADP和△CDP中,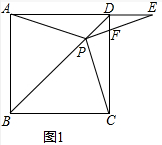
$\left\{\begin{array}{l}{AD=CD}\\{∠ADP=∠CDP}\\{DP=DP}\end{array}\right.$,
∴△ADP≌△CDP
∴PA=PC,
∵PA=PE,
∴PC=PE.
(2)证明:四边形ABCD为正方形,
∴∠ADC=∠CDE=90°,
∴∠E+∠DFE=90°,
∵PA=PE,
∴∠PAD=∠E,
由(1)知△ADP≌△CDP,
∴∠PAD=∠PCD,
∴∠PCD=∠E,∵∠PFC=∠DFE,
∴∠PCD+∠PFC=∠E+∠DFE=90°,
∴∠CPE=90°,
∴∠BPC+∠DPE=90°,
∵PD=DE,
∴∠DPE=∠E,
∴∠DPE=∠PCD,
∵∠BCP+∠PCD=90°,
∴∠BPC=∠BCP,
∴BP=BC. 
(3)∠BAP=∠DCE,
∵四边形ABCD是菱形,BD是对角线,
∴AB=BC,∠ABP=∠PBC,∠BAD=∠BCD,
在△ABP和△CBP中,
$\left\{\begin{array}{l}{BP=BP}\\{∠ABP=∠CBP}\\{AB=BC}\end{array}\right.$,
∴△ABP≌△CBP,
∴PA=PC,∠BAP=∠BCP,
∴∠PAD=∠PCD
∵PA=PE,
∴PC=PE,∠PAE=∠PEA,
∴∠PEA=∠PCD,
∵∠EFC=∠CPE+∠PCD=∠CDE+∠PEA,
∴∠CPE=∠CDE,
∵四边形ABCD为菱形,∠ABC=120°,
∴∠BCD=60°,∠ADC=120°,
∴∠CDE=60°,
∴∠CPE=60°,
∴△PCE是等边三角形,
∴∠PCE=60°,
∴∠BCP=∠DCE,
∴∠BAP=∠DCE.
点评 本题考查四边形综合题、正方形、菱形的性质、全等三角形的判定和性质,勾股定理等知识,正确寻找全等三角形是解题的关键,属于中考常考题型.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 等角的余角相等 | B. | 过一点作已知直线的垂线 | ||
| C. | 对顶角相等 | D. | 两直线平行,同位角相等 |
| A. | a:b:c=1:2:3 | B. | a+b=4,a+b+c=9 | C. | a=3,b=4,c=5 | D. | a:b:c=1:1:2 |
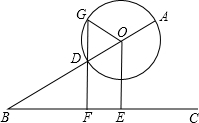 如图,线段AB与射线BC的夹角为30°,点O是AB上一动点,以点O为圆心,OA为半径作⊙O,交线段AB于另一点D,过点O作OE⊥BC于点E,过点D作直线DF⊥BC于点F,交⊙O于另一点G.
如图,线段AB与射线BC的夹角为30°,点O是AB上一动点,以点O为圆心,OA为半径作⊙O,交线段AB于另一点D,过点O作OE⊥BC于点E,过点D作直线DF⊥BC于点F,交⊙O于另一点G. 如图,在矩形ABCD中,AB<BC,M是BC的中点,DE⊥AM于点E,且AB、BC的长是一元二次方程x2-7x+12=0的两根,求△DEM的面积.
如图,在矩形ABCD中,AB<BC,M是BC的中点,DE⊥AM于点E,且AB、BC的长是一元二次方程x2-7x+12=0的两根,求△DEM的面积. 如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC.
如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC. 已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED.
已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED.