题目内容
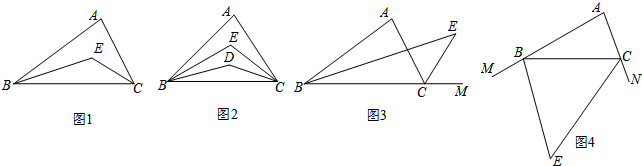
3.问题:如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=80°,则∠BEC=130°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.
探究:
(1)如图2,在△ABC中,BD、BE三等分∠ABC,CD、CE三等分∠ACB.若∠A=n°,则∠BEC=60°+$\frac{2}{3}$n°;
(2)如图3,在△ABC中,BE平分∠ABC,CE平分外角∠ACM.若∠A=n°,则∠BEC=$\frac{1}{2}$n°;
(3)如图4,在△ABC中,BE平分外角∠CBM,CE平分外角∠BCN.若∠A=n°,则∠BEC=90°-$\frac{1}{2}$n°.
分析 试题分析:问题:根据三角形内角和定理和角平分线的定义求解即可.
探究:(1)根据三角形内角和定理和三等分角的意义求解即可.
(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠E与∠1表示出∠2,然后整理即可得到∠BEC与∠E的关系.
(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB,然后再根据三角形的内角和定理列式整理即可得解.
解答 解:问题:如图1,∵BE、CE分别平分∠ABC和∠ACB,
∴∠EBC=$\frac{1}{2}$∠ABC,∠ECB=$\frac{1}{2}$∠ACB(角平分线的定义),
∴∠BEC=180°-(∠EBC+∠ECB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A;
若∠A=80°,则∠BEC=130°;若∠A=n°,则∠BEC=90°+$\frac{1}{2}$n°.
探究:(1)如图2,
∵线段BD、BE把∠ABC三等分,
∴∠EBC=$\frac{2}{3}$∠ABC;
又∵线段CD、CE把∠ACB三等分,
∴∠ECB=$\frac{2}{3}$∠ACB;
∴∠EBC+∠ECB=$\frac{2}{3}$(∠ABC+∠ACB)=$\frac{2}{3}$(180°-∠A),
∴∠BEC=180°-$\frac{2}{3}$(180°-∠A)=60°+∠A,
若∠A=n°,则∠BEC=60°+$\frac{2}{3}$n°;
(2)如图3,
∵BE和CE分别是∠ABC和∠ACM的角平分线,
∴∠EBC=$\frac{1}{2}$∠ABC,∠ACE=$\frac{1}{2}$∠ACM,
又∵∠ACM是△ABC的一外角,
∴∠ACM=∠A+∠ABC,
∴∠ACE=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠EBC,
∵∠ACM是△BEC的一外角,
∴∠BEC=∠ACE-∠EBC=$\frac{1}{2}$∠A+∠EBC-∠EBC=$\frac{1}{2}$∠A;
若∠A=n°,则∠BEC=$\frac{1}{2}$n°;
(3)如图4,
∵∠EBC=$\frac{1}{2}$(∠A+∠ACB),∠ECB=$\frac{1}{2}$(∠A+∠ABC),
∴∠BEC=180°-∠EBC-∠ECB,=180°-$\frac{1}{2}$(∠A+∠ACB)-$\frac{1}{2}$(∠A+∠ABC)
=180°-$\frac{1}{2}$∠A-$\frac{1}{2}$(∠A+∠ABC+∠ACB)=90°-∠A=90°-$\frac{1}{2}$n°.
故答案为问题:130°;90°+$\frac{1}{2}$n°;探究:(1)$60°+\frac{2}{3}n°$;(2)$\frac{1}{2}$n°;(3)90°-$\frac{1}{2}$n°.
点评 本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 如图,大小两个正方形的边长分别为a,b.求阴影部分的面积S(用含a,b的代数式表示).
如图,大小两个正方形的边长分别为a,b.求阴影部分的面积S(用含a,b的代数式表示). 如图,在平面直角坐标系中,O为坐标原点,B的坐标(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°
如图,在平面直角坐标系中,O为坐标原点,B的坐标(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°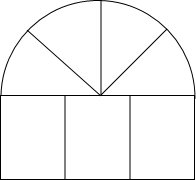 从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.
从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.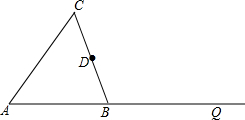 如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.