Question

18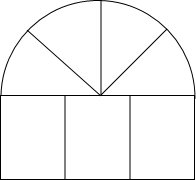．从房屋的窗户的形状如图所示，它的上部是四个小扇形组成的半圆，下部是有三个相同的小矩形组成，制作窗框的材料总长为15m，设半圆的半径为xm，窗户的截面面积为Sm²．
（1）求S与x之间的函数关系式，并求出x的取值范围；
（2）画出（1）中所求函数的图象；
（3）当x的长度为多少时，S有最大的值？最大的值是多少？（精确到0.01）

Answer 1

分析 （1）先设圆半径、矩形的宽和窗户的面积，再根据给出的已知条件列出它们的函数关系式；
（2）根据（1）中的函数关系式画出函数图象；
（3）根据函数图象直接得到答案．

解答 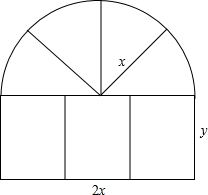解：（1）设半圆的半径为xm，矩形的宽为ym，窗户的面积为Sm²．
∵材料的总长为15m，
∴4y+7x+πx=15，
∴y=$\frac{1}{4}$（15-7x-πx），
从而S=2x•$\frac{1}{4}$（15-7x-πx）=-3.5x²+7.5x．即S=-3.5x²+7.5x；

（2）由（1）知S=-3.5x²+7.5x=-0.5x（7x-1.5）=-$\frac{7}{2}$（x-$\frac{15}{14}$）²+$\frac{225}{56}$，
则函数图象与x轴的两个交点坐标是（0，0）、（1.5，0），顶点坐标是（$\frac{15}{14}$，$\frac{225}{56}$），开口方向向下．
其大致图象如图所示：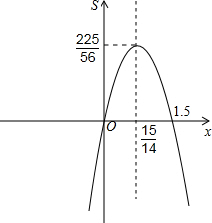
；

（3）如图所示，当x=$\frac{15}{14}$≈1.07时，S_最大值=$\frac{225}{56}$≈4.02．
答：当半圆的半径约为l.07m时，窗户通过的光线最多，此时窗户的面积约为4.02m²．

点评 本题考查了二次函数的性质在实际生活中的应用．最大销售利润的问题常利函数的增减性来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．其中要注意应该在自变量的取值范围内求最大值（或最小值），也就是说二次函数的最值不一定在x=$-\frac{b}{2a}$时取得．