题目内容
20.$\sqrt{3}$tan30°•$\sqrt{(\sqrt{3}-2)^2}$+${(\frac{1}{5})}^{-1}$.分析 根据特殊角的三角函数值以及利用二次根式的性质、负整数指数幂的性质分别化简,各数进而得出答案.
解答 解:原式=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$×(2-$\sqrt{3}$)+5
=2-$\sqrt{3}$+5
=7-$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
15.已知∠α的两边分别与∠β的两边垂直,且∠α=20°,则∠β的度数为( )
| A. | 20° | B. | 160° | C. | 20°或160° | D. | 70° |
12.宁波轨道交通2号线于2015年9月26日通车,全长50千米,50千米用科学记数法表示为( )
| A. | 5×104米 | B. | 5×125米 | C. | 50×103米 | D. | 50×104米 |
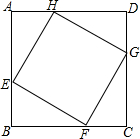 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB,BC,CD,DA上的动点,且AE=BF=CG=DH,