题目内容
8.分式方程:$\frac{x}{x+2}-1=\frac{8}{{4-{x^2}}}$的解为x=6.分析 去分母化为整式方程后求解即可.
解答 解:方程两边同时乘以(2+x)(2-x)得:
x(2-x)-(2+x)(2-x)=8,
整理得:2x-4=8,
解得:x=6,
检验:当x=6时,(2+x)(2-x)≠0,
所以方程的解为x=6.
点评 本题考查了分式方程的解法,解题的关键是能够确定最简公分母并去分母化为整式方程,注意一定要检验.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.对于每个正整数n,抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于An,Bn两点,以|AnBn|表示该两点间的距离,则|A1B1|+|A2B2|+…+|A2016B2016|的值是( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2016}{2017}$ |
13.已知A(1,1)、B(3,2),点B绕点A逆时针旋转90°到达点C处,则点C的坐标是( )
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
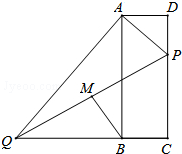 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.


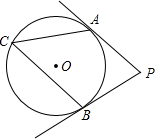 如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.
如图,PA、PB分别切⊙O于点A、B,若∠C=55°,则∠P的大小为70度.