题目内容
3.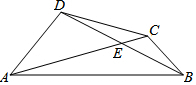 如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.
如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.
分析 如图,延长BC交AD的延长线于F,在AE上取一点K,使得EK=CE,连接DK、BK.由四边形CDKB是平行四边形,推出DK=BC=2,DK∥BF,由∠ACB=120°,推出∠FCA=180°-120°=60°,由∠DAC=30°,推出∠F=90°,∠ADK=∠F=90°,由∠DAK=30°,推出AK=2DK=4,由此即可解决问题.
解答 解:如图,延长BC交AD的延长线于F,在AE上取一点K,使得EK=CE,连接DK、BK.
∵DE=BE,EK=CE,
∴四边形CDKB是平行四边形,
∴DK=BC=2,DK∥BF,
∵∠ACB=120°,
∴∠FCA=180°-120°=60°,
∵∠DAC=30°,
∴∠F=90°,
∵DK∥BF,
∴∠ADK=∠F=90°,∵∠DAK=30°,
∴AK=2DK=4,
∴AC=AK+EK+CE=4+1+1=6,
故答案为6.
点评 本题考查平行四边形的判定和性质、直角三角形30度角性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考填空题中的压轴题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
20.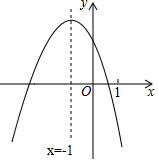 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠-1);③关于x的一元二次方程ax2+(b-1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:①4a+c<0;②m(am+b)+b>a(m≠-1);③关于x的一元二次方程ax2+(b-1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )


| A. | ab>0 | B. | $\frac{a}{b}>0$ | C. | a-1>0 | D. | a<b |
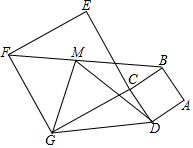 如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.
如图,正方形ABCD和正方形CEFG的面积分别为4平方厘米和36平方厘米,∠DCG=90°,M是BF的中点,则三角形DMG的面积为5平方厘米.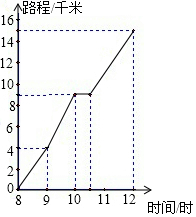 图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题:
图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图象回答问题: