题目内容
20.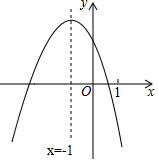 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:①4a+c<0;②m(am+b)+b>a(m≠-1);③关于x的一元二次方程ax2+(b-1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①根据对称轴列式,得b=2a,由图象可知:左交点的横坐标大于-3,当x=-3时,y<0,代入可得结论正确;
②开口向下,则顶点坐标的纵坐标是最大值,那么y=am2+bm+c<a-b+c,化简可得结论不正确;
③计算△的值作判断;
④比较k2与k2+1的值,根据当x>-1时,y随x的增大而减小,由图象得出结论.
解答 解:①因为二次函数的对称轴是直线x=-1,由图象可得左交点的横坐标大于-3,小于-2,
所以-$\frac{b}{2a}$=-1,
b=2a,
当x=-3时,y<0,
即9a-3b+c<0,
9a-6a+c<0,
3a+c<0,
∵a<0,
∴4a+c<0,
所以此选项结论正确;
②∵抛物线的对称轴是直线x=-1,
∴y=a-b+c的值最大,
即把x=m(m≠-1)代入得:y=am2+bm+c<a-b+c,
∴am2+bm<a-b,
m(am+b)+b<a,
所以此选项结论不正确;
③ax2+(b-1)x+c=0,
△=(b-1)2-4ac,
∵a<0,c>0,
∴ac<0,
∴-4ac>0,
∵(b-1)2≥0,
∴△>0,
∴关于x的一元二次方程ax2+(b-1)x+c=0有实数根;
④由图象得:当x>-1时,y随x的增大而减小,
∵当k为常数时,0≤k2≤k2+1,
∴当x=k2的值大于x=k2+1的函数值,
即ak4+bk2+c>a(k2+1)2+b(k2+1)+c,
ak4+bk2>a(k2+1)2+b(k2+1),
所以此选项结论不正确;
所以正确结论的个数是1个,
故选D.
点评 本题考查二次函数与系数关系,在解题时,注意二次函数的系数与其图象的形状、对称轴,特殊点的关系,灵活掌握二次函数的性质是解决问题的关键,学会利用图象信息解决问题,属于中考常考题型.

练习册系列答案
相关题目
10.已知三角形的两边长分别为5和7,则第三边长不可能是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
7.将向东行进30米,记作+30米,则向东行进-30米表示的意义是( )
| A. | 向东行进30米 | B. | 向东行进-30米 | C. | 向西行进30米 | D. | 向西行进-30米 |
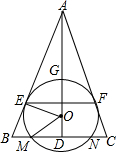 如图,O为等腰三角形ABC内一点,⊙O与底边BC交于M、N两点,且与AB、AC相切于E、F两点,连接AO,与⊙O交于点G,与BC相交于点D.
如图,O为等腰三角形ABC内一点,⊙O与底边BC交于M、N两点,且与AB、AC相切于E、F两点,连接AO,与⊙O交于点G,与BC相交于点D.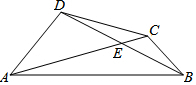 如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.
如图,四边形ABCD中,两对角线相交于E,且E为对角线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,则AC的长为6.