题目内容
 如图,D是AC上一点,BE∥AC,AE分别交BD、BC于点F、G.若∠1=∠2,线段BF、FG、FE之间有怎样的关系?请说明理由.
如图,D是AC上一点,BE∥AC,AE分别交BD、BC于点F、G.若∠1=∠2,线段BF、FG、FE之间有怎样的关系?请说明理由.考点:相似三角形的判定与性质
专题:
分析:根据BE∥AC,可得∠1=∠E,然后有∠1=∠2,可得∠2=∠E,又由∠GFB=∠BFE,可得出△BFG∽△EFB,最后可得出BF2=FG•FE.
解答:解:BF2=FG•FE.
理由:∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠GFB=∠BFE,
∴△BFG∽△EFB,
∴
=
,
即BF2=FG•FE.
理由:∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠GFB=∠BFE,
∴△BFG∽△EFB,
∴
| BF |
| EF |
| FG |
| BF |
即BF2=FG•FE.
点评:本题考查了相似三角形的判定与性质,解答本题的关键是根据BE∥AC,得出∠1=∠E,进而判定△BFG∽△EFB.

练习册系列答案
相关题目
一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )
| A、极差是15 |
| B、众数是88 |
| C、中位数是86 |
| D、平均数是87 |
 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=3:1,AC=12,求EC的长度.
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=3:1,AC=12,求EC的长度. 已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.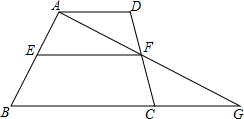 如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且
如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且