题目内容
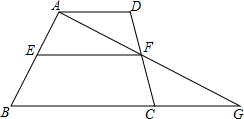如图，已知在梯形ABCD中，AD∥BC，E、F分别在AB、CD边上的点，AF交BC的延长线于点G，且| AE |
| BE |
| DF |
| FC |
| 2 |
| 3 |
考点：相似三角形的判定与性质
专题：
分析：根据平行线分线段成比例定理求出BG的长，再根据BC=9，求出CG的长，从而得出AD的长．
解答：解：∵AD∥BC，
∴
=
=
=
，
∵
=
，
∴
=
，
∴EF∥BG，
∴
=
=
，
∴
=
，
∴BG=15，
∴CG=6，
∴
=
，
∴AD=4．
∴
| AD |
| CG |
| DF |
| CF |
| AF |
| FG |
| 2 |
| 3 |
∵
| AE |
| BE |
| DF |
| CF |
∴
| AE |
| BE |
| AF |
| FG |
∴EF∥BG，
∴
| EF |
| BG |
| AE |
| AB |
| 2 |
| 5 |
∴
| 6 |
| BG |
| 2 |
| 5 |
∴BG=15，
∴CG=6，
∴
| AD |
| 6 |
| 2 |
| 3 |
∴AD=4．
点评：此题考查了相似三角形的判定与性质，利用平行线分线段成比例定理求出BG的长是解决本题的关键．
练习册系列答案
相关题目
如图，D是AC上一点，BE∥AC，AE分别交BD、BC于点F、G．若∠1=∠2，线段BF、FG、FE之间有怎样的关系？请说明理由．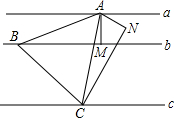
有一组平行线a∥b∥c，过点A作AM⊥b于M，作∠MAN=60°，且AN=AM，过点N作CN⊥AN交直线c于点C，在直线b上取点B使BM=CN，则△ABC为
定义：如果二次函数y=ax2+bx+c的最小值大于0，我们就说这个二次函数的值恒大于0．
如图，数轴的单位长度为1，如果B、C表示的数的和为2，那么A、D表示的数的和是（ ）| A、5 | B、4 | C、3 | D、2 |
小明用纸（如图）折成一个正方体的盒子，里面装入礼物，混放在下面的盒子里，请观察，礼物所在的盒子是（ ）
如图，在Rt△ABC中，∠ABC=90°，CD⊥BC，BD与AC相交于点E，AB=9，BC=4，DC=3．