题目内容
11.观察下列关于自然数的等式:(1)32-4×12=5 (1)
(2)52-4×22=9 (2)
(3)72-4×32=13 (3)
…
根据上述规律解决下列问题:
(1)完成第五个等式:112-4×52=21;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
分析 (1)根据前三个找出规律,写出第五个等式;
(2)用字母表示变化规律,根据完全平方公式计算,即可证明.
解答 解:(1)112-4×52=21,
故答案为:5;21;
(2)第n个等式为:(2n+1)2-4n2=4n+1,
证明:(2n+1)2-4n2=4n2+4n+1-4n2=4n+1.
点评 本题考查的是整式的混合运算、数字的变化,掌握整式的混合运算法则、正确找出数字的变化规律是解题的关键.

练习册系列答案
相关题目
1.已知P(x1,y1)、Q(x2,y2)是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,下列结论中错误的是( )
| A. | 如果x1、x2同号.那么点P、Q在同一象限 | |
| B. | 如果y1、y2异号.那么点P、Q在不同象限 | |
| C. | 如果k>0.且x1>x2,那么y1<y2 | |
| D. | 如果k<0.且x1<0,x2>0,那么y1>y2 |
1.下列计算正确的是( )
| A. | 5-2=-10 | B. | x2•x3=5x | C. | $\root{3}{{8}^{0}}$=2 | D. | (a2b)3=a6b3 |
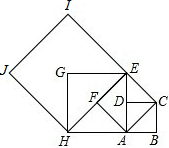 如图,已知四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第2个正方形ACEF,再以第2个正方形的对角线AE为边作第3个正方形AEGH,如此下去,则第n个正方形的面积Sn=2n-1.
如图,已知四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第2个正方形ACEF,再以第2个正方形的对角线AE为边作第3个正方形AEGH,如此下去,则第n个正方形的面积Sn=2n-1. 如图,在数轴上,点A和点B之间表示的整数有-1,0,1,2.
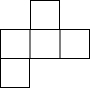
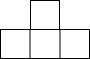
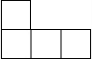
如图,在数轴上,点A和点B之间表示的整数有-1,0,1,2.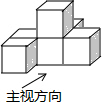 由六个相同的立方体拼成的几何体如图所示,则它的主视图是( )
由六个相同的立方体拼成的几何体如图所示,则它的主视图是( )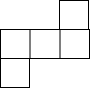
 如图,△ABC中,∠BAC、∠ABC、∠ACB的外角分别记为∠α,∠β,∠γ,若∠α:∠β:∠γ=3:4:5,则∠BAC:∠ABC:∠ACB等于3:2:1.
如图,△ABC中,∠BAC、∠ABC、∠ACB的外角分别记为∠α,∠β,∠γ,若∠α:∠β:∠γ=3:4:5,则∠BAC:∠ABC:∠ACB等于3:2:1.