题目内容
15. 如图,已知直线AB:y=k1x-2(k1≠0)与x轴交于点C,与双曲线y=$\frac{{k}_{2}}{x}$(k2≠0)交于点A、B,其中B点坐标为(m,-4),tan∠OCB=$\frac{2}{3}$.
如图,已知直线AB:y=k1x-2(k1≠0)与x轴交于点C,与双曲线y=$\frac{{k}_{2}}{x}$(k2≠0)交于点A、B,其中B点坐标为(m,-4),tan∠OCB=$\frac{2}{3}$.(1)求直线AB和双曲线的表达式;
(2)连接AO,BO,求△AOB的面积.
分析 (1)根据tan∠OCB=$\frac{2}{3}$,求得C的坐标和B的坐标,然后运用待定系数法分别求其解析式;
(2)把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算;
解答 解:由直线AB:y=k1x-2(k1≠0)可知D(0,-2),
∴OD=2,
∵tan∠OCB=$\frac{2}{3}$.
∴$\frac{OD}{OC}$=$\frac{2}{3}$,
∴OC=3,
∴C(-3,0),
代入y=k1x-2得:-3k1-2=0,
解得k1=-$\frac{2}{3}$,
∴直线AB为:y=-$\frac{2}{3}$x-2;
∵B(m,-4),tan∠OCB=$\frac{2}{3}$.
∴BE=4,
∴$\frac{BE}{CE}$=$\frac{2}{3}$,
∴CE=6,
∴OE=3,
∴B(3,-4),
∵B点在反比例函数的图象上,
∴k2=3×(-4)=-12.
∴双曲线的表达式为y=-$\frac{12}{x}$.
(2)解$\left\{\begin{array}{l}{y=-\frac{12}{x}}\\{y=-\frac{2}{3}x-2}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-6}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-4}\end{array}\right.$,
∴A(-6,2),
∵C(-3,0),
∴OC=3.
∴S△AOB=S△ACO+S△BCO=$\frac{1}{2}$×3×2+$\frac{1}{2}$×3×4=8.
点评 本题考查了一次函数和反比例函数的交点问题,用待定系数法确定一次函数和反比例函数的比例系数,求出函数解析式;要能够熟练借助直线和y轴的交点运用分割法求得不规则图形的面积.


 如图,AB∥CD,∠A=38°,∠C=∠E,则∠C的度数为19°.
如图,AB∥CD,∠A=38°,∠C=∠E,则∠C的度数为19°.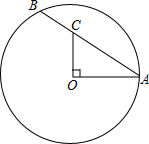 如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC
如图,⊙O的半径OA=5cm,AB是弦,C是AB上一点,且OC⊥OA,OC=BC