题目内容
17.(1)已知a、b互为相反数,m、n互为倒数,x的绝对值为2,求-2mn+$\frac{a+b}{m-n}$-x2的值.(2)如图所示,化简|a-c|+|a-b|+|c|

分析 (1)利用相反数,倒数,以及绝对值的代数意义求出a+b,mn以及x2的值,代入原式计算即可得到结果;
(2)根据数轴上点的位置确定出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:(1)根据题意得:a+b=0,mn=1,|x|=2,则x2=4,
所以原式=-2+0-4=-6;
(2)∵c<a<0<b,
∴a-c>0,a-b<0,
∴原式=a-c-a+b-c=b-2c.
点评 此题考查了整式数的加减,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.也考查了代数式求值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
3.已知a1=x-1(x≠1且x≠2),a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$,则a2016等于( )
| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
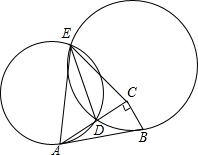 给定直角三角形ABC,点D是AC边上任意一点.两个圆与直线AB分别相切于点A和B,这两个圆交于D和E两点.求证:∠BAC=∠DEC.
给定直角三角形ABC,点D是AC边上任意一点.两个圆与直线AB分别相切于点A和B,这两个圆交于D和E两点.求证:∠BAC=∠DEC.