题目内容
8.数学活动:折纸、画图与探究:
问题情境:在矩形纸片ABCD中,AB=6,BC=10,折叠矩形纸片ABCD,使B落在边AD(不与A重合)上,落点记为E,这是折痕与边CD或者边BC(含端点)交于点F,与边AB或者边AD(含端点)交于点G,然后展开铺平,则四边形BFEG称为矩形ABCD的“折痕四边形”.
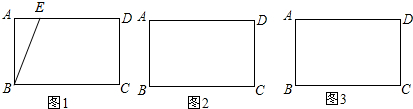
操作探究:
(1)如图1,当点E在图1的位置时,请作出此时的“折痕四边形”BFEG(要求:尺规作图,不写作法,保留作图痕迹),此时,图1中的等腰三角形有△BFE、△BGE;
(2)在折叠矩形的过程中,借助图2探究:
当点E是AD的中点时,折痕四边形BFEG的边EG的长为$\frac{61}{12}$;
当AE=6时,折痕四边形BFEG是正方形;
当AE取值范围是6<AE≤10时,折痕四边形BFEG是非正方形的菱形;
(3)在折叠矩形的过程中,当点F在线段CD上时,如图3,设AE的长度为x,折痕四边形BFEG的面积是y,求y与x的函数关系式,并直接写出x的取值范围.
分析 (1)根据尺规作图的一般步骤作图,根据翻折变换的性质得到等腰三角形;
(2)根据折叠的性质、勾股定理和正方形的性质求出AE;根据菱形的判定和性质求出AE的取值范围;
(3)设EG=BG=m,根据题意和全等三角形的判定和性质求出y与x的函数关系式.
解答 解:(1)如图1,四边形BFEG是所求作的折痕四边形,
由折叠的性质可知在:△BFE、△BGE是等腰三角形;
(2)如图2,∵点E是AD的中点,
∴AE=$\frac{1}{2}$AD=5,
由折叠的性质,BG=EG,
设EG=x,则BG=x,AG=6-x,
由勾股定理得,AG2+AE2=EG2,
即(6-x)2+25=x2,
解得,x=$\frac{61}{12}$,即EG=$\frac{61}{12}$;
当折痕四边形BFEG是正方形时,
BG=EG,BG⊥EG,
∴点G与点A重合,
∴AE=AB=6;
如图3,当AE>6时,
由题意得,GB=GE,FE=FB,∠BGF=∠EGF,
∵AD∥BC,
∴∠EGF=∠GFB,
∴∠BGF=∠GFB,
∴BG=BF,
∴BG=GE=EF=FG,
∴四边形BFEG是菱形,
∴当6<AE≤10时,四边形BFEG是菱形;
故答案为:$\frac{61}{12}$;6;6<AE≤10;
(3)如图1,∵点B的对称点是点E,
∴EG=BG,
设EG=BG=m,则AG=6-m,
由勾股定理得,m2=x2+(6-m)2,
化简得,m=$\frac{1}{12}$x2+3,
∵点B与点E关于直线GC对称,
∴△BFG≌△EFG,
∴四边形BFEG的面积=2×△BFG的面积,
即S=2×($\frac{1}{12}$x2+3)×10=$\frac{5}{6}$x2+30,(0<x≤2).
点评 本题考查的是矩形的性质、翻折变换的性质和函数解析式的确定,掌握翻折变换的性质:对应边相等、对应角相等是解题的关键.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案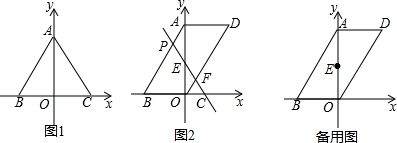
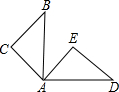 如图,已知△ABC≌△ADE,∠B=42°,∠C=90°,∠EAB=40°,则∠BAD=88°.
如图,已知△ABC≌△ADE,∠B=42°,∠C=90°,∠EAB=40°,则∠BAD=88°.