题目内容
6.已知关于x的一元二次方程(m-1)x2-(2m+2)x+m+4=0有两个不相等的实数根,(1)求实数m的取值范围;
(2)若两实数根的倒数和为S,直接写出S的范围.
分析 (1)首先利用根的判别式大于0,且m-1≠0,求得m的取值范围;
(2)设方程的两个根式a b,由根与系数的关系得a+b=$\frac{2m+2}{m-1}$,ab=$\frac{m+4}{m-1}$,代入S=$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$,求出即可.
解答 解:(1)∵关于x的一元二次方程(m-1)x2-(2m+2)x+m+4=0有两个不相等的实数根,
∴△=b2-4ac=(2m+2)2-4×(m-1)(m+4)=-4m+20>0,m-1≠0,
解得:m<5,m≠1;
(2)∵设方程的两个根是a b,
∴a+b=$\frac{2m+2}{m-1}$,ab=$\frac{m+4}{m-1}$,
∴S=$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{2m+2}{m+4}$,
∵m<5,
∴S<$\frac{4}{3}$.
点评 本题考查了根与系数的关系和根的判别式,注意:如果m n是一元二次方程ax2+bx+c=0(a≠0)的两个根,则m+n=-$\frac{b}{a}$,mn=$\frac{c}{a}$.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 观察右面由“※”组成的图案和算式.解答问题.
观察右面由“※”组成的图案和算式.解答问题. 如图,点E,F,G,H在长方形ABCD的四条边上,已知∠1=∠2=30°,∠3=20°.求五边形EFGCH各个内角的度数.
如图,点E,F,G,H在长方形ABCD的四条边上,已知∠1=∠2=30°,∠3=20°.求五边形EFGCH各个内角的度数.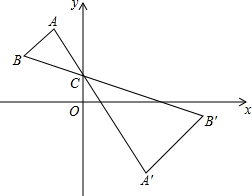 如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b).
如图,点A、B、C在平面直角坐标系xOy中,点A的坐标为(a,b),点C的坐标为(0,1),△A′B′C是△ABC关于点C的位似图形.若△ABC与△A′B′C的相似比为1:2,则点A′的坐标为(-2a,3-2b). 如图所示,在△ABC中,AB=AC,∠BAC=90°,AD是BC边上的中线,且AD=4cm,则BC=8cm.
如图所示,在△ABC中,AB=AC,∠BAC=90°,AD是BC边上的中线,且AD=4cm,则BC=8cm.