如图.已知△ABC≌△ADE.∠B=42°.∠C=90°.∠EAB=40°.则∠BAD=88°．题目和参考答案——青夏教育精英家教网—

题目内容

17．

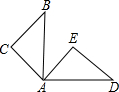如图，已知△ABC≌△ADE，∠B=42°，∠C=90°，∠EAB=40°，则∠BAD=88°．

分析先利用全等的性质得∠D=∠B=42°，∠E=∠C=90°，再根据三角形内角和定理计算出∠DAE=48°，然后计算∠DAE+∠EAB即可．

解答解：∵△ABC≌△ADE，
∴∠D=∠B=42°，∠E=∠C=90°，
∴∠DAE=180°-∠E-∠D=180°-90°-42°=48°，
∴∠BAD=∠DAE+∠EAB=48°+40°=88°．
故答案为88°．

点评本题考查了全等三角形的性质：全等三角形的对应边相等，全等三角形的对应角相等．

练习册系列答案

相关题目

15．

如图所示，在△ABC中，AB=AC，∠BAC=90°，AD是BC边上的中线，且AD=4cm，则BC=8cm．

8．数学活动：
折纸、画图与探究：
问题情境：在矩形纸片ABCD中，AB=6，BC=10，折叠矩形纸片ABCD，使B落在边AD（不与A重合）上，落点记为E，这是折痕与边CD或者边BC（含端点）交于点F，与边AB或者边AD（含端点）交于点G，然后展开铺平，则四边形BFEG称为矩形ABCD的“折痕四边形”．

操作探究：
（1）如图1，当点E在图1的位置时，请作出此时的“折痕四边形”BFEG（要求：尺规作图，不写作法，保留作图痕迹），此时，图1中的等腰三角形有△BFE、△BGE；
（2）在折叠矩形的过程中，借助图2探究：
当点E是AD的中点时，折痕四边形BFEG的边EG的长为$\frac{61}{12}$；
当AE=6时，折痕四边形BFEG是正方形；
当AE取值范围是6＜AE≤10时，折痕四边形BFEG是非正方形的菱形；
（3）在折叠矩形的过程中，当点F在线段CD上时，如图3，设AE的长度为x，折痕四边形BFEG的面积是y，求y与x的函数关系式，并直接写出x的取值范围．

5．下列方程中是关于x的一元二次方程的是（　　）

A．

ax²+bx+c=0

B．

$\frac{1}{{x}^{2}}$+$\frac{2}{x}$=3

12．

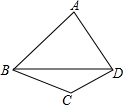如图，四边形ABCD中，∠ABC=3∠CBD，∠ADC=3∠CDB，∠C=130°，则∠A的度数是（　　）

2．如果自行车车条的长度比标准长度长3mm，记作+3mm，那么比标准长度短1.2mm，应记作-1.2mm．

9．用两种方法计算：（$\frac{1}{3}-\frac{5}{6}+\frac{7}{9}$）$÷（-\frac{1}{18}）$．

7．

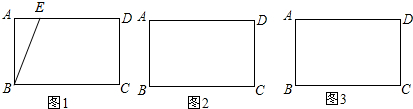
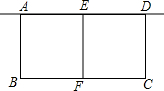如图是一个矩形养鸡场的平面图，养鸡场由一堵旧墙（旧墙的长度不小于l米）和总长为l0米的篱笆围成，中间用篱笆分隔成两个小矩形．设大矩形的垂直于旧墙的一边长为x米，面积为s平方米．求s关于x的函数解析式，并写出这个函数的定义域．

试题分类