题目内容
12. 如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:
如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:(1)△ABD≌△ACE;
(2)OB=OC.
分析 (1)由已知条件得到∠BAD=∠CAE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到∠ABD=∠ACE,由等腰三角形的性质得到∠ABC=∠ACB由角的和差即可得到∠OBC=∠OCB,然后根据等腰三角形的判定即可得到结论.
解答 证明:(1)∵∠BAE=∠CAD,
∴∠BAD=∠CAE,
在△ABD与△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC-∠ABD=∠ACB-∠ACE,
即∠OBC=∠OCB,
∴OB=OC.
点评 此题考查了全等三角形的判定与性质,等腰三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
2.某服装店用7000元购进A、B两种新式服装,按标价售出后获得毛利润4000元(毛利润=售价-进价),这两种服装的进价,标价如表所示:
求这两种服装各购进的件数?
| 类型 价格 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 150 |
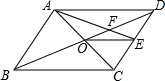 如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6.
如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6. 如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE.
如图,△BDC与△CEB在线段BC的同侧,CD与BE相交于点A,∠ABC=∠ACB,AD=AE,求证:BD=CE. 如图,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B
如图,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B 在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒. 在平面直角坐标系中,已知抛物线y=ax2+bx-4经过A(-4,0),C(2,0)两点.
在平面直角坐标系中,已知抛物线y=ax2+bx-4经过A(-4,0),C(2,0)两点.