题目内容
3.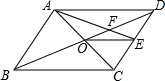 如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6.
如图,点O是?ABCD的对角线交点,E为CD中点,AE交BD于点F,若S△AOE=3,则S△AOB的值为6.
分析 直接利用平行四边形的性质得出O是AC的中点,即可得出S△AOE=S△EOC,再利用三角形中位线定理得出EO∥AD,则S△AOE=S△DOE,进而求出答案.
解答 解:∵点O是?ABCD的对角线交点,
∴O是AC的中点,则S△AOE=S△EOC,
又∵E为CD中点,
∴EO是△ACD的中位线,
∴EO∥AD,
∴S△AOE=S△DOE,
∴S△DOC=3+3=6,
故S△AOB的值为6.
故答案为:6.
点评 此题主要考查了平行四边形的性质以及三角形中线以及三角形中位线的性质,得出S△AOE=S△DOE是解题关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
11. 如图所示,下列条件中,①∠1=∠4;②∠2=∠4;③∠1=∠3;④∠5=∠4,其中能判断直线l1∥l2的有( )
如图所示,下列条件中,①∠1=∠4;②∠2=∠4;③∠1=∠3;④∠5=∠4,其中能判断直线l1∥l2的有( )
 如图所示,下列条件中,①∠1=∠4;②∠2=∠4;③∠1=∠3;④∠5=∠4,其中能判断直线l1∥l2的有( )
如图所示,下列条件中,①∠1=∠4;②∠2=∠4;③∠1=∠3;④∠5=∠4,其中能判断直线l1∥l2的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列语句不正确的是( )
| A. | 在同一平面内,过直线外一点有且只有一条直线与已知直线平行. | |
| B. | 两直线被第三直线所截,如果同位角相等,那么两直线平行 | |
| C. | 两点确定一条直线 | |
| D. | 内错角相等 |
 如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.
 如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:
如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证: