题目内容
2.某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加2株,平均单株盈利就减少0.5元,则每盆植7株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植7或9株.分析 根据已知假设每盆花苗(原来花盆中有3株)增加a(a为偶数)株,盈利为y元,则每盆花苗有(a+3)株,得出平均单株盈利为(3-0.5×$\frac{a}{2}$)元,由题意得y=(a+3)(3-0.5×$\frac{a}{2}$),根据二次函数的性质即可求得.
解答 解:设每盆花苗(假设原来花盆中有3株)增加a(a为偶数)株,盈利为y元,
则根据题意得:y=(3-0.5×$\frac{a}{2}$)(a+3)
=-$\frac{1}{4}$(a-$\frac{9}{2}$)2+$\frac{225}{16}$,
∵a为偶数,
∴a=4,
∵当a=2时,y=12.5<13
当a=4时,y=(2-0.5×$\frac{4}{2}$)+(4+3)=14>13,
当a=6时,y=(2-0.5×$\frac{6}{2}$)+(6+3)=13.5>13,
∴每盆植7株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植7或9株.
故答案为7、7或9.
点评 此题考查了二次函数的应用,根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键.

练习册系列答案
相关题目
17.我市农业结构调整取得了巨大成功,今年水果又喜获丰收,某果园组织30辆汽车装运A、B、C三种水果共84t到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的汽车辆数不超过装运的A、C两种水果的汽车辆数之和.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
(2)设此次外销活动的利润为Q(百元),求Q与x之间的函数关系式,请你提出一个获得最大利润时的车辆分配方案.
(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
11.数学活动课上,小敏、小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF,那么它们的大小关系是( )
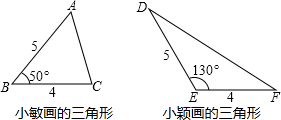

| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
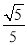 B.
B. 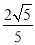 C.
C. 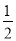 D. 2
D. 2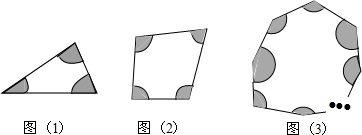
 由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )
由几个大小相同的小正方体组成的立体图形的俯视图如左图所示,则这个立体图形应是图中的( )



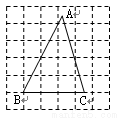
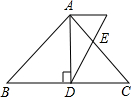 如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.