题目内容
11.数学活动课上,小敏、小颖分别画了△ABC和△DEF,尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF,那么它们的大小关系是( )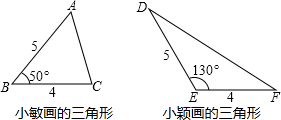
| A. | S△ABC>S△DEF | B. | S△ABC<S△DEF | C. | S△ABC=S△DEF | D. | 不能确定 |
分析 在两个图形中分别作BC、EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.
解答 解:如图,过点A、D分别作AG⊥BC,DH⊥EF,垂足分别为G、H,
在Rt△ABG中,AG=ABsinB=5×sin 50°=5sin 50°,
在Rt△DHE中,∠DEH=180°-130°=50°,
DH=DEsin∠DEH=5sin 50°,
∴AG=DH.
∵BC=4,EF=4,
∴S△ABC=S△DEF.
故选C.
点评 本题考查了解直角三角形中的正弦函数的应用以及等底等高两三角形面积相等,求得三角形的高相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.甲、乙两商场同时开业,为了吸引顾客,都举办有奖酬宾活动,凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外,其他全部相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券的多少(如下表).
甲商场:
乙商场:
(1)请你用列表法(或画树状图)求出摸到一红一白的概率;
(2)如果只考虑中奖因素,你将会选择去哪个商场购物?请说明理由.
甲商场:
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
(2)如果只考虑中奖因素,你将会选择去哪个商场购物?请说明理由.
16.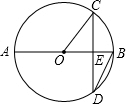 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )| A. | $\frac{3}{2}$cm | B. | 3cm | C. | 2$\sqrt{3}$cm | D. | 9cm |
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
 如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为8-2π.
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为8-2π.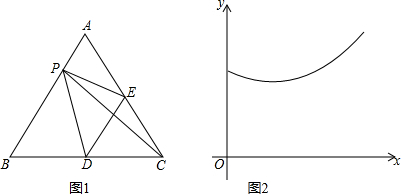
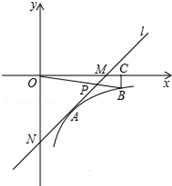 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,
如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,