题目内容
14.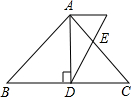 如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
如图,AD是等腰△ABC底边上的高,且AD=4,sinB=$\frac{4}{5}$,若E是AC边上的点,且满足AE:EC=2:3,连接DE,求cot∠ADE的值.
分析 作AF∥BC交DE的延长线于F,如图,根据等腰三角形的性质得BD=CD,AB=AC,在Rt△ABD中利用∠B的正弦可求出AB=5,再利用勾股定理可计算出BD=3,所以CD=3,AC=5,然后通过△AEF∽△CED,利用相似比可计算出AF=2,然后在Rt△DAF中,根据余切的定义求解.
解答 解:作AF∥BC交DE的延长线于F,如图,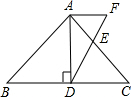
∵AD是等腰△ABC底边上的高,
∴BD=CD,AB=AC,
在Rt△ABD中,∵sinB=$\frac{AD}{AB}$=$\frac{4}{5}$,而AD=4,
∴AB=5,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=3,
∴CD=3,AC=5,
∵AF∥CD,
∴∠DAF=90°,△AEF∽△CED,
∴$\frac{AF}{CD}$=$\frac{AE}{EC}$,即$\frac{AF}{3}$=$\frac{2}{3}$,
∴AF=2,
在Rt△DAF中,cot∠ADF=$\frac{AD}{AF}$=$\frac{4}{2}$=2,
即cot∠ADE的值为2.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了相似三角形的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.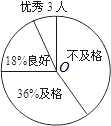 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?
 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?
 按要求作图并回答问题:
按要求作图并回答问题: 已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B.
已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B. 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.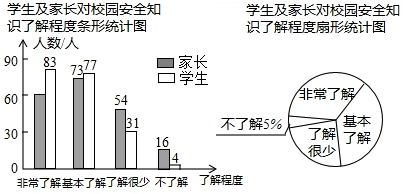
 如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为8-2π.
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为8-2π.