题目内容
10．如图，在三角形各顶点作半径为1的圆（每两个圆都相互外离），则图中三个扇形的面积和为$\frac{π}{2}$，在四边形各顶点作半径为1的圆（每两个圆都相互外离），则图中四个扇形的面积和为π；在2015边形的每一个顶点作半径为1的圆（每两个圆都相互外离），则2015边形中扇形的面积和为$\frac{2013}{2}$π．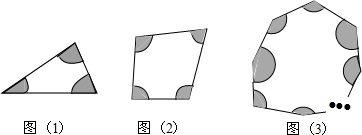
分析 根据题意结合多边形内角和定理以及扇形面积公式求出即可．
解答 解：如图所示：2015边形的内角和为：（2015-2）×180°=2013×180°，
则2015边形中扇形的面积和为：$\frac{2013×180π×{1}^{2}}{360}$=$\frac{2013}{2}$π．
故答案为：$\frac{2013}{2}$π．
点评 此题主要考查了扇形面积公式以及多边形内角和定理，得出多边形的内角和是解题关键．
练习册系列答案
相关题目
1．甲、乙两商场同时开业，为了吸引顾客，都举办有奖酬宾活动，凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外，其他全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少（如下表）．
甲商场：
乙商场：
（1）请你用列表法（或画树状图）求出摸到一红一白的概率；
（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．
甲商场：
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 10 | 5 | 10 |
（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．
5．
李明对某校九年级（2）班进行了一次社会实践活动调查，从调查的内容中抽出两项．
调查一：对小聪、小亮两位同学的毕业成绩进行调查，其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算，计算的方法按4：4：2进行，毕业成绩达80分以上为“优秀毕业生”，小聪、小亮的三项成绩如右表：（单位：分）
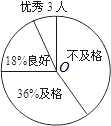
调查二：对九年级（2）班50名同学某项跑步成绩进行调查，并绘制了一个不完整的扇形统计图，请你根据以上提供的信息，解答下列问题：
（1）小聪和小亮谁能达到“优秀毕业生”水平？哪位同学的毕业成绩更好些？
（2）升入高中后，请你对他俩今后的发展给每人提一条建议．
（3）扇形统计图中“优秀率”是多少？
（4）“不及格”在扇形统计图中所占的圆心角是多少度？
李明对某校九年级（2）班进行了一次社会实践活动调查，从调查的内容中抽出两项．调查一：对小聪、小亮两位同学的毕业成绩进行调查，其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算，计算的方法按4：4：2进行，毕业成绩达80分以上为“优秀毕业生”，小聪、小亮的三项成绩如右表：（单位：分）
| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
（1）小聪和小亮谁能达到“优秀毕业生”水平？哪位同学的毕业成绩更好些？
（2）升入高中后，请你对他俩今后的发展给每人提一条建议．
（3）扇形统计图中“优秀率”是多少？
（4）“不及格”在扇形统计图中所占的圆心角是多少度？
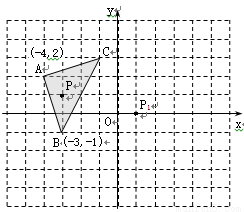
如图，若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点，且OC=2BD．则实数k的值为4$\sqrt{3}$．