题目内容
17.我市农业结构调整取得了巨大成功,今年水果又喜获丰收,某果园组织30辆汽车装运A、B、C三种水果共84t到外地销售,规定每辆汽车只装运一种水果,且必须装满;又装运每种水果的汽车不少于4辆;同时,装运的B种水果的汽车辆数不超过装运的A、C两种水果的汽车辆数之和.(1)设用x辆汽车装运A种水果,用y辆汽车装运B种水果,根据下表提供的信息,求y与x之间的函数关系式并直接写出自变量x的取值范围;
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
分析 (1)关键描述语:某乡组织30辆汽车装运A、B、C三种水果共84吨到外地销售,根据每辆汽车运装量和汽车的辆数,可列出y与x之间的函数关系式,再根据装运每种水果的汽车不少于4辆,装运的B种水果的重量不超过装运的A、C两种水果重量之和.
可将自变量x的取值范围求出;
(2)根据水果品种每吨水果的利润和销售的数量,可将此次外销活动的利润Q表示出来,根据x的取值范围,从而将最大利润时车辆的分配方案求出.
解答 解:(1)由题得到:4x+3y+2(30-x-y)=84,所以y=-2x+24,
又因为x≥4,y≥4,30-x-y≥4,
则-2x+24≥4,30-x-(-2x+24)≥4,
得到-2≤x≤10;
∵y≤x+30-x-y,y=-2x+24,
∴x≥4.5,
∴4.5≤x≤10;
(2)Q=6×4x+8×3y+5×2(30-x-y)=-6x+540,
Q随着x的减小而增大,又因为4.5≤x≤10,所以当x=5时,Q取得最大值,即Q=5×4×6+14×3×8+11×2×5(元)=566(百元),
此时应这样安排:A水果用5辆车,B水果用14辆车,C水果用11辆车.
点评 本题主要考查一次函数在实际生活中的应用,在解题过程中应确定未知量的取值范围.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
8. 一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )
一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )
 一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )
一次函数y=(m+2)x+(1+m)的图象如图所示,则m的取值范围是( )| A. | m>-1 | B. | m<-2 | C. | -2<m<-1 | D. | m<-1 |
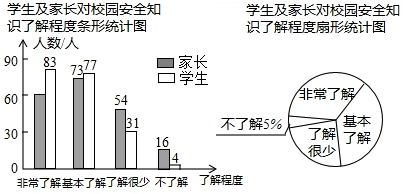
5. 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
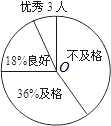
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,请你根据以上提供的信息,解答下列问题:
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?
 李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.
李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项.调查一:对小聪、小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
| 综合素质 | 考试成绩 | 体育测试 | |
| 满分 | 100 | 100 | 100 |
| 小聪 | 72 | 98 | 60 |
| 小亮 | 90 | 75 | 95 |
(1)小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)升入高中后,请你对他俩今后的发展给每人提一条建议.
(3)扇形统计图中“优秀率”是多少?
(4)“不及格”在扇形统计图中所占的圆心角是多少度?
7.为了解我县九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:40分;B:39-35分;C:34-30分;D:29-20分;E:19-0分)统计如表:
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为32,c的值为0.05;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问甲同学体育成绩应在什么分数段内?B(填相应分数段的字母);
(3)若把成绩在35分以上(含35分)定位优秀,则我县今年8500名九年级学生中体育成绩为优秀的学生人数约有多少名?
| 分数段 | 人数(人) | 频率 |
| A | 48 | 0.48 |
| B | a | 0.32 |
| C | b | 0.10 |
| D | c | d |
| E | e | 0.05 |
(1)在统计表中,a的值为32,c的值为0.05;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问甲同学体育成绩应在什么分数段内?B(填相应分数段的字母);
(3)若把成绩在35分以上(含35分)定位优秀,则我县今年8500名九年级学生中体育成绩为优秀的学生人数约有多少名?
 +18 B. 3
+18 B. 3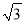 +9 C. 2
+9 C. 2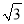 +18 D.
+18 D. 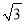 +9
+9 由几个相同的小正方体组成了一个几何体,该几何体的三视图如图所示,则该几何体可能为( )
由几个相同的小正方体组成了一个几何体,该几何体的三视图如图所示,则该几何体可能为( )



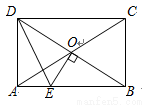
 已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B.
已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B.