题目内容
7.在平面直角坐标系中,点C沿着某条路径运动,以点C为旋转中心,将点A(0,4)逆时针方向旋转60°,到点B(m,1).若-5≤m≤5,则点C的运动路径长为10.分析 根据旋转的性质得到△AB1C1,△AB2C2是等边三角形,推出△B1AB2≌△C1AC2,根据全等三角形的性质得到B1B2=C1C2,∠1=∠2,求得∠3=∠4=60°,于是得到当B1,B2在直线y=1上时,点C的路径与直线y=1成60°的角,根据已知条件即可得到结论.
解答  解:由旋转的性质得,C1B1=AC1,C2B2=AC2,∵∠B1C1A=∠B2C2A=60°,
解:由旋转的性质得,C1B1=AC1,C2B2=AC2,∵∠B1C1A=∠B2C2A=60°,
∴△AB1C1,△AB2C2是等边三角形,
∴AB1=AC1,AB2=AC2,∠B1AC1=∠B2AC2=60°,
∴∠B1AB2=∠C1AC2,
在△B1AB2与△C1AC2中,$\left\{\begin{array}{l}{A{B}_{1}=A{B}_{2}}\\{∠{B}_{1}A{B}_{2}=∠{C}_{1}A{C}_{2}}\\{A{C}_{1}=A{C}_{2}}\end{array}\right.$,
∴△B1AB2≌△C1AC2,
∴B1B2=C1C2,∠1=∠2,
∴∠3=∠4=60°,
∴当B1,B2在直线y=1上时,点C的路径与直线y=1成60°的角,
∵-5≤m≤5,
∴C1C2=B1B2=10,
即点C的运动路径长为10,
故答案为:10.
点评 本题考查了旋转的性质,全等三角形的判定和性质,轨迹,正确的作出图形是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
17.已知a>b,且c为非零实数,那么下列结论一定正确的是( )
| A. | ac<bc | B. | ac2<bc2 | C. | ac>bc | D. | ac2>bc2 |
15.下列图形中,不是正方体平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列运算正确的是( )
| A. | (-2a2b)3=8a5b3 | B. | a2-3a2=-2a2 | C. | a•(-a2)=a3 | D. | a8÷a4=a2 |
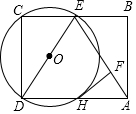 如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.
如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F. 已知反比例函数y=$\frac{5-m}{x}$(m为常数)的图象经过点A(1,6).
已知反比例函数y=$\frac{5-m}{x}$(m为常数)的图象经过点A(1,6).