题目内容
7.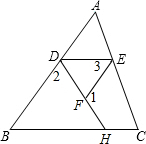 完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴∠EFD=∠2(同角的补角相等)①
∴AB∥EF(内错角相等,两直线平行)②
∴∠ADE=∠3(两直线平行,内错角相等)③
∵∠3=∠B(已知)④
∴∠ADE=∠B(等量代换)⑤
∴DE∥BC(同位角相等,两直线平行)⑥
∴∠AED=∠C(两直线平行,同位角相等)⑦
分析 首先根据∠1+∠EFD=180°和∠1+∠2=180°可以证明∠EFD=∠2,再根据内错角相等,两直线平行可得AB∥EF,进而得到∠ADE=∠3,再结合条件∠3=∠B可得∠ADE=∠B,进而得到DE∥BC,再由平行线的性质可得∠AED=∠C.
解答 解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴∠EFD=∠2(同角的补角相等)①
∴AB∥EF(内错角相等,两直线平行)②
∴∠ADE=∠3(两直线平行,内错角相等)③
∵∠3=∠B(已知)④
∴∠ADE=∠B(等量代换)⑤
∴DE∥BC(同位角相等,两直线平行)⑥
∴∠AED=∠C(两直线平行,同位角相等)⑦.
故答案为:∠EFD=∠2;AB∥EF;两直线平行,内错角相等;已知;∠ADE=∠B;同位角相等,两直线平行;两直线平行,同位角相等.
点评 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.

练习册系列答案
相关题目
2.某公园的门票价格如下表所示:
某校七年级(1)、(2)两个班去游览该公园,其中(1)班人数不足50人,(2)班人数超过50人且少于100人,但两个班合起来人数超过100人.如果两个班都以班为单位分别购票,则一共应付910元;如果两个班联合起来,作为一个团体购票,则只需付612元.
(1)求七年级(1)、(2)两个班分别有多少学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
| 购票张数 | 1~50张 | 51~100张 | 100张以上 |
| 每张票价格 | 10元 | 8元 | 6元 |
(1)求七年级(1)、(2)两个班分别有多少学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
12.下列二次根式能与$\sqrt{6}$合并的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{24}$ | D. | $\sqrt{30}$ |
16.下列图形既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.
如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.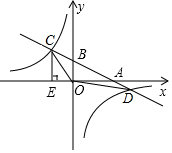 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E. 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的纵坐标为8.