题目内容
5.一元二次方程两个根为1和3,那么这个方程为( )| A. | x2+4x+3=0 | B. | x2+4x-3=0 | C. | x2-4x+3=0 | D. | x2-4x-3=0 |
分析 结合选项设出一元二次方程为x2+ax+b=0,根据根与系数的关系可找出关于a、b的二元一次方程组,解方程组即可得出结论.
解答 解:根据选项可设一元二次方程为x2+ax+b=0,
∵该方程两个根为1和3,
∴有$\left\{\begin{array}{l}{-a=1+3}\\{b=1×3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-4}\\{b=3}\end{array}\right.$.
即该一元二次方程为x2-4x+3=0.
故选C.
点评 本题考查了根与系数的关系以及用待定系数法求方程系数,解题的关键是找出关于a、b的二元一次方程组.本题属于基础题,难度不大,只要牢牢记住根与系数的关系即可得出结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.用因式分解法解一元二次方程x(x-3)=x-3时,原方程可化为( )
| A. | (x-1)(x-3)=0 | B. | (x+1)(x-3)=0 | C. | x (x-3)=0 | D. | (x-2)(x-3)=0 |
13.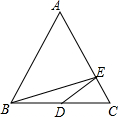 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{3}+1$ |
17.下列运算中错误的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$ | C. | $\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{{{(\sqrt{2}-\sqrt{3})}^2}}=\sqrt{2}-\sqrt{3}$ |
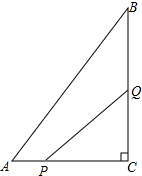 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?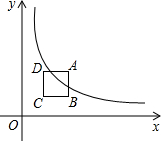 在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3.
在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3.