题目内容
10. 在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.
分析 由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数,又由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数.
解答 解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠ACE=$\frac{1}{2}$∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,
∠ECD=90°-70°=20°
点评 此题考查了三角形的内角和定理,三角形外角的性质以及三角形高线,角平分线的定义等知识.此题难度不大,解题的关键是数形结合思想的应用.

练习册系列答案
相关题目
5. 如图,在长方形ABCD中,CD与BC的长度比为5:12,若该长方形的周长为34,则BD的长为( )
如图,在长方形ABCD中,CD与BC的长度比为5:12,若该长方形的周长为34,则BD的长为( )
 如图,在长方形ABCD中,CD与BC的长度比为5:12,若该长方形的周长为34,则BD的长为( )
如图,在长方形ABCD中,CD与BC的长度比为5:12,若该长方形的周长为34,则BD的长为( )| A. | 13 | B. | 12 | C. | 8 | D. | 10 |
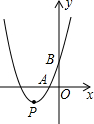 如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$.
如图,抛物线y=x2+bx+3顶点为P,且分别与x轴、y轴交于A、B两点,点A在点P的右侧,tan∠ABO=$\frac{1}{3}$.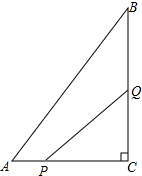 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2?
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从A点开始沿AC边向点C以1cm/s的速度运动,在C点停止,点Q从C点开始沿CB方向向点B以2cm/s的速度运动,在点B停止.如果点P、Q分别从A、C同时出发,经过几秒,△PCQ的面积是8cm2? 如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.
如图,己知∠1=∠2,AC=AD,增加一个条件能使△ABC≌△AEDAB=AE.