题目内容
如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,点P是x轴上的一个动点(不与原点O重合),以线段AP为一边,在其右侧作等边三角形△APQ.
(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否改变?如不改变,求出其大小;如改变,请说明理由.
(3)是否存在点P,使得△OBQ是等腰三角形?若存在,请直接写出所有符合条件P点坐标;若不存在,请说明理由.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否改变?如不改变,求出其大小;如改变,请说明理由.
(3)是否存在点P,使得△OBQ是等腰三角形?若存在,请直接写出所有符合条件P点坐标;若不存在,请说明理由.

考点:全等三角形的判定与性质,坐标与图形性质,等腰三角形的判定,等边三角形的性质
专题:
分析:(1)如图,作辅助线;证明∠BOC=30°,OB=2,借助直角三角形的边角关系即可解决问题.
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题.
(3)根据题意,结合图形,直接写出P点坐标即可解决问题.
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题.
(3)根据题意,结合图形,直接写出P点坐标即可解决问题.
解答: 解:(1)如图1,过点B作BC⊥x轴于点C.
解:(1)如图1,过点B作BC⊥x轴于点C.
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2;
∴∠BOC=30°,而∠OCB=90°,
∴BC=
OB=1,OC=
,
∴点B的坐标为B(
,1).
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB;
在△APO与△AQB中,
,
∴△APO≌△AQB(SAS).
∴∠ABQ=∠AOP=90°.
(3)存在,点P坐标为P(-4,0)、P(4,0).
 解:(1)如图1,过点B作BC⊥x轴于点C.
解:(1)如图1,过点B作BC⊥x轴于点C.∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2;
∴∠BOC=30°,而∠OCB=90°,
∴BC=
| 1 |
| 2 |
| 3 |
∴点B的坐标为B(
| 3 |
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB;
在△APO与△AQB中,
|
∴△APO≌△AQB(SAS).
∴∠ABQ=∠AOP=90°.
(3)存在,点P坐标为P(-4,0)、P(4,0).
点评:该题以平面直角坐标系、等边三角形为载体,以全等三角形的判定及其性质、等边三角形的性质等几何知识点为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
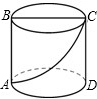 如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).
如图所示,是一圆柱体,已知圆柱的高AB=3,底面直径BC=10,现在有一只蚂蚁想要从A处沿圆柱表面爬行到对角C处去捕食,则它爬行最短路径是( )(本题π取3).| A、13 | ||
B、3
| ||
C、
| ||
D、2
|
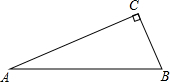 如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )
如图,Rt△ABC中,∠C=90°,∠B=α,将△ABC绕点C逆时针旋转得到△A′B′C,当点A′落在直线AB上时,旋转角为β(其中0°<β<180°),那么β与α之间的数量关系为( )| A、β=180°-α | ||
| B、β=90°+α | ||
C、β=
| ||
| D、β=2α |
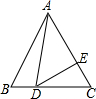 如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=
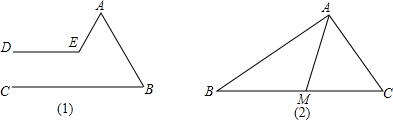
如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=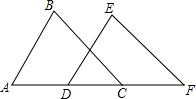 如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.
如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.