题目内容
 如图,四边形ABCD是长方形,E为AD上一点,连接BE,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求△DFG的面积.
如图,四边形ABCD是长方形,E为AD上一点,连接BE,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求△DFG的面积.考点:矩形的性质
专题:
分析:欲求△DFG的面积,由G是FC的中点,可以得到S△DFG=
S△DFC,由F是BE的中点,AB=10.AE=6.ED=2可以求得相应的△DEF,△DGC,△BCF的面积,继而求得答案.
| 1 |
| 2 |
解答: 解:如图,在矩形ABCD中,∠A=90°.
解:如图,在矩形ABCD中,∠A=90°.
过F作FH垂直AD于H.
∵F是BE的中点,
∴BF=FE,FH∥AB,所以FH=FM,
∵AB=10,AE=8,
∴S△ABE=
AE•AB=
×8×10=40,
S△BCF=
,
△DFH的面积=
,
△DFC的面积是80-30-20-5=25,
G是FC的中点,
△DFG的面积是△DFC的面积的一半,
△DFG的面积是12.5;
答选:D.
 解:如图,在矩形ABCD中,∠A=90°.
解:如图,在矩形ABCD中,∠A=90°.过F作FH垂直AD于H.
∵F是BE的中点,
∴BF=FE,FH∥AB,所以FH=FM,
∵AB=10,AE=8,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCF=
| 1 |
| 2 |
△DFH的面积=
| 1 |
| 2 |
△DFC的面积是80-30-20-5=25,
G是FC的中点,
△DFG的面积是△DFC的面积的一半,
△DFG的面积是12.5;
答选:D.
点评:此题考查了矩形的性质,高一定时、三角形的面积与底成正比例的性质的灵活应用,解答此题的关键是利用辅助线进行等积变形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知二次函数y=-x2+2x+3图象的对称轴为直线.
已知二次函数y=-x2+2x+3图象的对称轴为直线. 如图,PA切⊙O于点A,OP=2,∠P=30°,弦AB∥OP.
如图,PA切⊙O于点A,OP=2,∠P=30°,弦AB∥OP.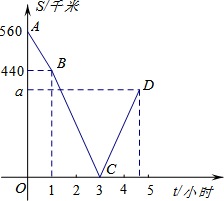 甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车才出发,并以各自速度匀速行驶,甲车出发3小时两车相遇,相遇后两车仍按原速度原方向各自行驶.如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间t(小时)之间的函数图象.则:
甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车才出发,并以各自速度匀速行驶,甲车出发3小时两车相遇,相遇后两车仍按原速度原方向各自行驶.如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间t(小时)之间的函数图象.则: