题目内容
4．
有理数m，n在数轴上的位置如图所示，那么化简|2m-2n|-$\sqrt{（n-m）^{2}}$的结果是m-n．
分析 根据数轴可以判断m、n的大小，从而可以化简|2m-2n|-$\sqrt{（n-m）^{2}}$，本题得以解决．
解答 解：由数轴可得，n＜0＜m，
∴m-n＞0，n-m＜0，
∴|2m-2n|-$\sqrt{（n-m）^{2}}$
=2m-2n-（m-n）
=2m-2n-m+n
=m-n，
故答案为：m-n．
点评 本题考查实数与数轴，解题的关键是明确数轴的特点，由数轴可以得到m、n的大小．
练习册系列答案
相关题目
14．下列说法中错误的是（ ）
| A． | 4的平方根是±2 | B． | 2是4的一个平方根 | ||
| C． | -2是4的一个平方根 | D． | 4的平方根是2 |
12．
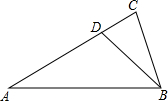如图，∠A=∠CBD=30°，∠ABD=45°，则以下结论错误的是（ ）
如图，∠A=∠CBD=30°，∠ABD=45°，则以下结论错误的是（ ）| A． | AB=3CD | B． | BC2=CD•AB | ||
| C． | △BCD是等腰三角形 | D． | 2CD=（$\sqrt{3}-1$）AD |
19．下列说法中错误的是（ ）
| A． | 9的算术平方根是3 | B． | 4的平方根是±2 | ||
| C． | 27的立方根是±3 | D． | 立方根等于-1的实数是-1 |
9．
如图，AB⊥BD，ED⊥BD，垂足分别为B、D，则下列各式中正确的是（ ）
如图，AB⊥BD，ED⊥BD，垂足分别为B、D，则下列各式中正确的是（ ）| A． | $\frac{EC}{AC}$=$\frac{BD}{DC}$ | B． | $\frac{AC}{AE}$=$\frac{BC}{DC}$ | C． | $\frac{EC}{BD}$=$\frac{AC}{DC}$ | D． | $\frac{AC}{EC}$=$\frac{BC}{DC}$ |