题目内容
3. 如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°.
如图,已知Rt△ABC中,∠BAC=90°,∠ACB=30°.(1)利用尺规作∠BAC的角平分线AD,交BC于点D(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求△ABD与△ACD的面积之比.
分析 (1)直接利用角平分线的作法得出答案;
(2)利用角平分线的性质结合三角形面积求法得出答案.
解答  解:(1)如图所示:AD即为所求;
解:(1)如图所示:AD即为所求;
(2)过点D作DE⊥AB于点E,DF⊥AC于点F,
∵AD平分∠BAC,
∴DE=DF,
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{\frac{1}{2}×AB×DE}{\frac{1}{2}×DF×AC}$=$\frac{AB}{AC}$=tan30°=$\frac{\sqrt{3}}{3}$.
点评 此题主要考查了角平分线的作法与性质,正确掌握角平分线的性质是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.下列说法中错误的是( )
| A. | 4的平方根是±2 | B. | 2是4的一个平方根 | ||
| C. | -2是4的一个平方根 | D. | 4的平方根是2 |
11.将甲乙两数据进行比较,如果甲的波动性大,那么( )
| A. | 甲的标准差小 | B. | 乙的方差小 | C. | 甲的平均数大 | D. | 乙的中位数小 |
8. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )| A. | 10$\sqrt{3}$+1 | B. | 10$\sqrt{3}$ | C. | 10.5 | D. | 11.5 |
12.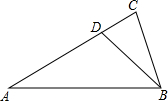 如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
 如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )
如图,∠A=∠CBD=30°,∠ABD=45°,则以下结论错误的是( )| A. | AB=3CD | B. | BC2=CD•AB | ||
| C. | △BCD是等腰三角形 | D. | 2CD=($\sqrt{3}-1$)AD |
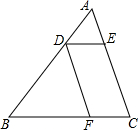 如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.
如图,在△ABC中,点D是AB边的三等分点(AD<BD),DE∥BC交AC于点E,DF∥AC交BC于点F,求$\frac{DE}{BF}$的值.