题目内容
9.解方程:$\frac{x-8}{x-3}$-$\frac{x-9}{x-4}$=$\frac{x+7}{x+8}$-$\frac{x+2}{x+3}$.分析 分式方程变形后,求出解,检验即可.
解答 解:方程变形得:$\frac{5}{x-4}$-$\frac{5}{x-3}$=$\frac{1}{x+3}$-$\frac{1}{x+8}$,
通分得:$\frac{5}{{x}^{2}-7x+12}$=$\frac{5}{{x}^{2}+11x+24}$,
则x2-7x+12=x2+11x+24,
解得x=-$\frac{2}{3}$,
经检验x=-$\frac{2}{3}$是分式方程的解;
所以,分式方程的解为x=-$\frac{2}{3}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
19.已知抛物线y=ax2+bx-2与x轴没有交点,过A(-$\frac{13}{7}$、y1)、B(-3,y2)、C(1,y2)、D($\sqrt{3}$,y3)四点,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y1>y3>y2 | D. | y3>y2>y1 |
9. 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )| A. | 45° | B. | 80° | C. | 100° | D. | 160° |
6.下面各式运用等式的性质变形,错误的是( )
| A. | 若x-3=y-3,则x=y | B. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | ||
| C. | 若a(c2+1)=b(c2+1),则a=b | D. | 若ac=bc,则a=b |
7.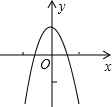 二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )
二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )
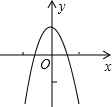 二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )
二次函数y=-3x2+1的图象如图所示,将其沿x轴翻折后得到的抛物线的解析式为( )| A. | y=-3x2-1 | B. | y=3x2 | C. | y=3x2+1 | D. | y=3x2-1 |

 如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC.
如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC.