题目内容
7．
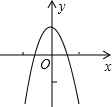二次函数y=-3x2+1的图象如图所示，将其沿x轴翻折后得到的抛物线的解析式为（ ）| A． | y=-3x2-1 | B． | y=3x2 | C． | y=3x2+1 | D． | y=3x2-1 |
分析 由于二次函数y=-3x2+1的图象沿x轴翻折后所得抛物线的开口大小与原抛物线的开口大小相同，只是开口方向相反，然后写出点（0，1）关于x轴的对称点的坐标，再利用顶点式即可得到新抛物线的解析式．
解答 解：二次函数y=-3x2+1的图象的顶点坐标为（0，1），
点（0，1）关于x轴的对称点的坐标为（0，-1），
又因为二次函数y=-3x2+1的图象沿x轴翻折后所得抛物线的开口大小与原抛物线的开口大小相同，只是开口方向相反，
所以所得抛物线的解析式为y=3x2-1．
故选D．
点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
阅读快车系列答案
相关题目
2．二次函数y=-2x2的图象如何移动就得到y=-2（x-1）2+3的图象（ ）
| A． | 向左移动1个单位，向上移动3个单位 | |
| B． | 向右移动1个单位，向上移动3个单位 | |
| C． | 向左移动1个单位，向下移动3个单位 | |
| D． | 向右移动1个单位，向下移动3个单位 |
19．将抛物线y=2x2向下平移1个单位，向右平移1个单位得到的抛物线是（ ）
| A． | y=2（x+1）2-1 | B． | y=2（x-1）2-1 | C． | y=2x2+1 | D． | y=2x2-1 |
17．若多项式5-（m+3）a+an是关于a的二次二项式，则mn的值是（ ）
| A． | -6 | B． | 6 | C． | -9 | D． | 9 |