题目内容
20.已知$\frac{a}{b}$=$\frac{2}{3}$,$\frac{b}{c}$=$\frac{2}{5}$,求$\frac{2a+b+c}{a-2b+c}$的值.分析 利用已知条件,用b分别表示a和c,再把a、c代入$\frac{2a+b+c}{a-2b+c}$中,然后把分子分母合并后约分即可.
解答 解:∵$\frac{a}{b}$=$\frac{2}{3}$,$\frac{b}{c}$=$\frac{2}{5}$,
∴a=$\frac{2}{3}$b,c=$\frac{5}{2}$b,
∴$\frac{2a+b+c}{a-2b+c}$=$\frac{\frac{4}{3}b+b+\frac{5}{2}b}{\frac{2}{3}b-2b+\frac{5}{2}b}$=$\frac{29}{7}$.
点评 本题考查了分式的值:解答时从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.

练习册系列答案
相关题目
11.(-a5)2+(-a2)5的结果是( )
| A. | 0 | B. | -2a7 | C. | 2a10 | D. | -2a10 |
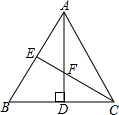 如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.
如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.