题目内容
2. 如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC.
如图,四边形ABCD,M、N分别为AB、CD的中点,P、Q是连线的交点.求证:S四边形MQNP=S△APD+S△BQC.
分析 连接AC,BD,根据四边形ABCD,M、N分别为AB、CD的中点,得到S△ADM=$\frac{1}{2}$S△ABD,S△BCM=$\frac{1}{2}$S△ABC,结合图形,利用等式的性质化简即可得证.
解答 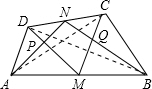 证明:连接AC,BD,
证明:连接AC,BD,
∵四边形ABCD,M、N分别为AB、CD的中点,
∴S△ADM=$\frac{1}{2}$S△ABD,S△BCM=$\frac{1}{2}$S△ABC,
S△DMC=S四边形ABCD-S△ADM-S△BCM
=($\frac{1}{2}$S四边形ABCD-S△ADM)+($\frac{1}{2}$S四边形ABCD-S△BCM)
=$\frac{1}{2}$S△ABD+$\frac{1}{2}$S△BCD-S△ADM+$\frac{1}{2}$S△ADC+$\frac{1}{2}$S△ACB-S△BCM
=S△ADM+$\frac{1}{2}$S△BCD-S△ADM+$\frac{1}{2}$S△ADC+S△BCM-S△BCM
=$\frac{1}{2}$S△BCD+$\frac{1}{2}$S△ADC
=S△BCN+S△ADN,
两边减去S△DPN+S△QCN得:S△DMC-(S△DPN+S△QCN)=S△BCN+S△ADN-(S△DPN+S△QCN),
即S四边形MQNP=S△APD+S△BQC.
点评 此题考查了面积及等积变换,弄清三角形的中线把三角形分为面积相等的两部分是解本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
7.三角形的外心具有的性质是( )
| A. | 到三边的距离相等 | B. | 外心一定在三角形外 | ||
| C. | 到三个顶点的距离相等 | D. | 外心一定在三角形内 |
14.抛物线y=x2-4x-4的对称轴是( )
| A. | x=-2 | B. | x=2 | C. | x=4 | D. | x=-4 |
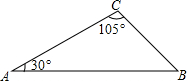 如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.
如图,已知AC=8,∠A=30°,∠C=105°,求AB和BC的长.