题目内容
4.已知A,B两点在数轴上表示的数为a和b,O为原点.(1)若A,B的位置如图1所示,
①用含a,b的式子表示A,B两点之间的距离为b-a;
②化简:|a|+|b|+|a-b|=2b-2a;
(2)如图2,M为AB中点,N为OA中点,且MN=2AB-15,a=-3.
①P为数轴上一点,若PA=$\frac{2}{3}$AB,试求点P对应的数为多少?
②在数轴上是否存在点Q,使得它表示的数x满足|x-a|+|x-b|=12?若存在,求出点Q;若不存在,说明理由.
③若关于x的方程|x-a|+|x-b|=m有解,直接写出m的取值范围.

分析 (1)①用B点表示的数减去A点表示的数即可得到A,B两点之间的距离;②先根据绝对值的意义去绝对值符合,然后合并即可;
(2)①利用线段的中点定义得到AM=$\frac{1}{2}$AB,AN=$\frac{1}{2}$AO,则MN=AM-AN=$\frac{1}{2}$OB=$\frac{1}{2}$b,所以$\frac{1}{2}$b=2(b+3)-15,解得b=6,则AB=9,PA=6,然后分类讨论:当P点在A点左侧时,P点表示的数为-9;当P点在A点右侧时,P点表示的数为3;②分类讨论:当x≤-3时,-x-3-x+6=12;当-3<x<6时,x+3-x+6=12;当x≥6时,x+3+x-6=12,然后分别解方程求出x即可得到Q点表示的数;③对于|x+3|+|x-6|=m,当x≤-3时,-x-3-x+6=m,解得x=$\frac{3-m}{2}$,利用x的取值范围得到$\frac{3-m}{2}$≤-3,解得m≥9;当-3<x<6时,x+3-x+6=m,易得m=9;当x≥6时,x+3+x-6=m,解得x=$\frac{m+3}{2}$,利用x的取值范围得到$\frac{m+3}{2}$≥6,解得m≥9,于是可判断m的取值范围为m≥9.
解答 解:(1)①A,B两点之间的距离为|b-a|=b-a;
②|a|+|b|+|a-b|=-a+b+b-a=2b-2a;
故答案为b-a,2b-2a;
(2)①∵M为AB中点,N为OA中点,
∴AM=$\frac{1}{2}$AB,AN=$\frac{1}{2}$AO,
∴MN=AM-AN=$\frac{1}{2}$AB-$\frac{1}{2}$AO=$\frac{1}{2}$OB=$\frac{1}{2}$b,
∵MN=2AB-15,a=-3,
∴$\frac{1}{2}$b=2(b+3)-15,解得b=6,
∴AB=6+3=9,
∵PA=$\frac{2}{3}$AB,
∴PA=$\frac{2}{3}$×9=6,
当P点在A点左侧时,P点表示的数为-9;
当P点在A点右侧时,P点表示的数为3;
②存在.
|x+3|+|x-6|=12,
当x≤-3时,-x-3-x+6=12,解得x=$\frac{3-m}{2}$,则$\frac{3-m}{2}$≤-3;
当-3<x<6时,x+3-x+6=12,无解;
当x≥6时,x+3+x-6=12,解得x=7.5,
所以满足条件的Q点表示的数为-4.5或7.5;
③|x+3|+|x-6|=m,
当x≤-3时,-x-3-x+6=m,解得x=$\frac{3-m}{2}$,则$\frac{3-m}{2}$≤-3,解得m≥9;
当-3<x<6时,x+3-x+6=m,m=9;
当x≥6时,x+3+x-6=m,解得x=$\frac{m+3}{2}$,则$\frac{m+3}{2}$≥6,解得m≥9
所以m的取值范围为m≥9.
点评 本题考查了绝对值:当a是正数时,a的绝对值是它本身a; 当a是负数时,a的绝对值是它的相反数-a; 当a是零时,a的绝对值是零.也考查了数轴.

 名校课堂系列答案
名校课堂系列答案①由四舍五入得到的近似数1.2万精确到十分位;
②实数与数轴上的点一一对应;
③在1和3之间的无理数有无数个;
④$\frac{π}{2}$是分数,它是有理数.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
| A. | 向左移动1个单位,向上移动3个单位 | |
| B. | 向右移动1个单位,向上移动3个单位 | |
| C. | 向左移动1个单位,向下移动3个单位 | |
| D. | 向右移动1个单位,向下移动3个单位 |
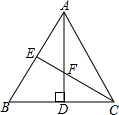 如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.
如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.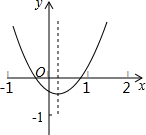 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=$\frac{1}{3}$,下列结论:①a>0,b<0,c>0;②a+b+c<0;③a-b+c>0;④2a-3b=0;其中正确的有③(只填写序号).
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=$\frac{1}{3}$,下列结论:①a>0,b<0,c>0;②a+b+c<0;③a-b+c>0;④2a-3b=0;其中正确的有③(只填写序号).