题目内容
9. 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )| A. | 45° | B. | 80° | C. | 100° | D. | 160° |
分析 根据圆内接四边形的性质可得∠A+∠BCD=180°,然后再计算出∠BCD的度数,进而可得∠A的度数,再根据圆周角定理可得答案.
解答 解:∵四边形ABCD内接于⊙O,
∴∠A+∠BCD=180°,
∵∠DCE=80°,
∴∠BCD=100°,
∴∠A=80°,
∴∠BOD=160°,
故选:D.
点评 此题主要考查了圆内接四边形的性质,以及圆周角定理,关键是掌握圆内接四边形的性质:圆内接四边形的对角互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.(-a5)2+(-a2)5的结果是( )
| A. | 0 | B. | -2a7 | C. | 2a10 | D. | -2a10 |
14.抛物线y=x2-4x-4的对称轴是( )
| A. | x=-2 | B. | x=2 | C. | x=4 | D. | x=-4 |
1.有下列说法:
①由四舍五入得到的近似数1.2万精确到十分位;
②实数与数轴上的点一一对应;
③在1和3之间的无理数有无数个;
④$\frac{π}{2}$是分数,它是有理数.
其中正确的是( )
①由四舍五入得到的近似数1.2万精确到十分位;
②实数与数轴上的点一一对应;
③在1和3之间的无理数有无数个;
④$\frac{π}{2}$是分数,它是有理数.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
19.将抛物线y=2x2向下平移1个单位,向右平移1个单位得到的抛物线是( )
| A. | y=2(x+1)2-1 | B. | y=2(x-1)2-1 | C. | y=2x2+1 | D. | y=2x2-1 |
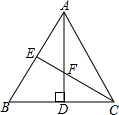 如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.
如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.