题目内容
3. 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )| A. | PC>0 | B. | 0<PC<12 | C. | 3≤PC≤12 | D. | 3<PC<12 |
分析 过点D作DF⊥BC于F点,分P点在F右侧和在线段BF上讨论,并比较当BE最大时是否有BE≤AB,由此得出结论.
解答 解:过点D作DF⊥BC于F点,如图,
①当P点在F点的右侧时,显然有∠DPB<90°,E点在线段AB的延长线上,不符合题意,此时0≤PC<3.
②当P点在线段BF中时,设BP=a,则PF=BF-BP=AD-BP=9-a,
∵∠BPE+∠EPD+∠DPF=180°,∠DPF+∠FDP=90°,
∴∠BPE=∠GDP,∠EBP=∠PFD=90°,
∴△BPE∽△FDP,
∴$\frac{BE}{BP}$=$\frac{PF}{FD}$,即BE=$\frac{9a-{a}^{2}}{10}$,
当a=$\frac{9}{2}$时,BE最大为$\frac{81}{40}$<10=AB,
∵BE≥0,
∴0≤a≤9,PC=BC-a,
∴3≤PC≤12.
综合①②得知3≤PC≤12.
故选C.
点评 本题考查了相似三角形的判定与性质定理,解题的关键是通过极值问题判定,当点P在线段BF上时,E点在线段AB上.

练习册系列答案
相关题目
6.高安市出租车司机小李某天营运全是在东西走向的320国道上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如表:
(1)将最后一名乘客送达目的地时,小李距下午出发地点的距离是多少千米?
(2)若汽车耗油量a升/千米,这天下午汽车耗油共多少升?
| +15 | -3 | +14 | -11 | +10 | -12 |
(2)若汽车耗油量a升/千米,这天下午汽车耗油共多少升?

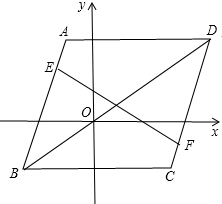 如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).
如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD). 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°.
如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°. 如图,已知∠AOB=60°,∠AOC=∠BOC,OD是∠COB的角平分线,求∠COD的度数.
如图,已知∠AOB=60°,∠AOC=∠BOC,OD是∠COB的角平分线,求∠COD的度数.