题目内容
6. 请将下列说理过程补充完整:
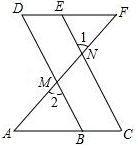
请将下列说理过程补充完整:已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=∠2,∠A=∠F.
试说明:∠C=∠D.
理由:因为∠1=∠2(已知),
又因为∠1=∠ANC(对顶角相等),所以∠2=∠ANC(等量代换).
所以BD∥CE(同位角相等,两直线平行),所以∠ABD=∠C(两直线平行,同位角相等).
又因为∠A=∠F(已知),所以DF∥AC.(内错角相等,两直线平行)所以∠ABD=∠D(两直线平行,内错角相等).
所以∠C=∠D(等量代换).
分析 根据两直线平行,同位角相等,即可得出∠ABD=∠C,再根据两直线平行,内错角相等,即可得出∠ABD=∠D,进而得到∠C=∠D.
解答  解:因为∠1=∠2(已知),
解:因为∠1=∠2(已知),
又因为∠1=∠ANC(对顶角相等 ),
所以∠2=∠ANC(等量代换),
所以 BD∥CE(同位角相等,两直线平行),
所以∠ABD=∠C( 两直线平行,同位角相等 ),
又因为∠A=∠F(已知),
所以 DF∥AC(内错角相等,两直线平行 ),
所以∠ABD=∠D(两直线平行,内错角相等),
所以∠C=∠D( 等量代换 ).
故答案为:对顶角相等,∠2=∠ANC,BD,CE,两直线平行,同位角相等,DF,AC,内错角相等,两直线平行,∠ABD=∠D,等量代换.
点评 本题主要考查了平行线的性质与判定,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
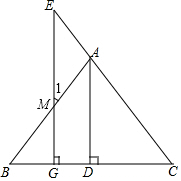 如图,若AD⊥BC,EG⊥BC,∠1=∠E,则AD为∠BAC的平分线,请你说明理由.
如图,若AD⊥BC,EG⊥BC,∠1=∠E,则AD为∠BAC的平分线,请你说明理由.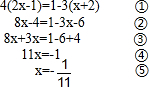
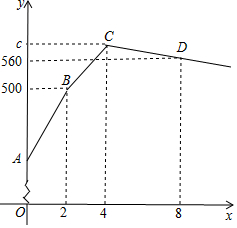 某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.
某手工编织厂生产一种旅游纪念品,现有60名工人进行手工编织(每人编织的效率相同),2天后抽出10名工人执行其他任务,其余工人继续编织生产;2天后从编织的工人中再抽出10名进行销售(每人每天的销售量相同).已知每人每天的销售量是编织量的5倍,下图是产品库存量y(件)与生产时间x(天)之间的函数关系图象.