题目内容
1．
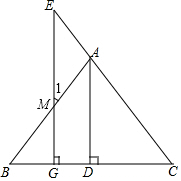如图，若AD⊥BC，EG⊥BC，∠1=∠E，则AD为∠BAC的平分线，请你说明理由．
分析 首先要根据平行线的判定证明两条直线平行，再根据平行线的性质证明有关的角相等，运用等量代换的方法证明AD所分的两个角相等，即可证明．
解答 证明：∵AD⊥BC，EG⊥BC，
∴AD∥EG，
∴∠DAC=∠E，∠1=∠BAD，
∵∠E=∠1，
∴∠BAD=∠CAD（等量代换），
∴AD是∠BAC的平分线（角平分线定义）．
点评 本题主要考查了平行线的判定与性质以及角平分线的定义的运用，解决问题的关键是掌握：两直线平行，同位角相等，内错角相等．
练习册系列答案
相关题目
11．下列命题中，其逆命题成立的是（ ）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c，满足a2+b2=c2，那么这个三角形是直角三角形．
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长a，b，c，满足a2+b2=c2，那么这个三角形是直角三角形．
| A． | ①④ | B． | ①②④ | C． | ②③ | D． | ①③ |
9．下列二次根式中，是最简二次根式的是（ ）
| A． | $\sqrt{4}$ | B． | $\sqrt{\frac{1}{5}}$ | C． | $\sqrt{10}$ | D． | $\sqrt{0.5}$ |
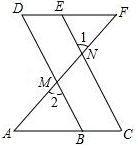请将下列说理过程补充完整：
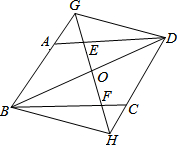如图，在平行四边形ABCD中，AB=3，BC=4，∠ABC=60°，过对角线BD的中点O的直线GH分别交AD、BC于点E、F，交BA的延长线于点G，交DC的延长线于点H，连结GD、BH，则下列结论：①AG=CH，②DE+CF=5，③S四边形ABFE=3$\sqrt{3}$，④四边形BGDH为平行四边形．其中正确的有（ ）