题目内容
16.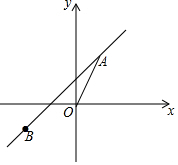 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).(1)求一次函数的解析式;
(2)请直接写出不等式组-1<kx+b<2x的解集.
分析 (1)由点A的纵坐标利用正比例函数图象上点的坐标特征可求出点A的坐标,根据点A、B的坐标,利用待定系数法即可求出一次函数的解析式;
(2)根据一次函数的性质结合点B的坐标可得出不等式-1<x+1的解集为x>-2,再根据两函数图象的上下位置关系,即可得出不等式组-1<x+1<2x的解集为x>1.
解答 解:(1)∵点A(m,2)在正比例函数y=2x的图象上,
∴2=2m,解得:m=1,
∴点A的坐标为(1,2).
将A(1,2)、B(-2,-1)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=2}\\{-2k+b=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为y=x+1.
(2)∵在y=x+1中,1>0,
∴y值随x值的增大而增大,
∴不等式-1<x+1的解集为x>-2.
观察函数图象可知,当x>1时,一次函数y=x+1的图象在正比例函数y=2x的图象的下方,
∴不等式组-1<x+1<2x的解集为x>1.
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征、一次函数与一元一次不等式以及一次函数的性质,解题的关键是:(1)根据点的坐标,利用待定系数法即可求出一次函数的解析式;(2)根据一次函数的性质结合两函数图象的上下位置关系,找出不等式组-1<x+1<2x的解集.

练习册系列答案
相关题目
4. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
1.已知?ABCD中,∠B+∠D=200°,则∠A的度数为( )
| A. | 100° | B. | 160° | C. | 80° | D. | 60° |
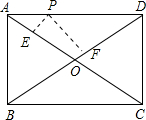 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )