题目内容
5.化简:$\frac{5a+3b}{{a}^{2}-{b}^{2}}$-$\frac{2a}{{a}^{2}-{b}^{2}}$.分析 根据分式的减法可以解答本题.
解答 解:$\frac{5a+3b}{{a}^{2}-{b}^{2}}$-$\frac{2a}{{a}^{2}-{b}^{2}}$
=$\frac{5a+3b-2a}{(a+b)(a-b)}$
=$\frac{3(a+b)}{(a+b)(a-b)}$
=$\frac{3}{a-b}$.
点评 本题考查分式的减法,解答本题的关键是明确分式的减法的计算方法.

练习册系列答案
相关题目
16.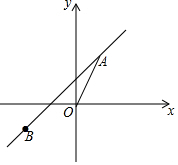 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).
(1)求一次函数的解析式;
(2)请直接写出不等式组-1<kx+b<2x的解集.
 如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(-2,-1).(1)求一次函数的解析式;
(2)请直接写出不等式组-1<kx+b<2x的解集.
10.若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )
| A. | 2 | B. | 8 | C. | -2 | D. | -8 |
17.下列图标是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.能使式子$\sqrt{2-x}$+$\sqrt{x-1}$成立的x的取值范围是( )
| A. | x≥1 | B. | x≥2 | C. | 1≤x≤2 | D. | x≤2 |
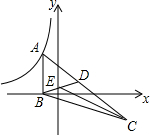 如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.
如图,△ABC的顶点A在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AB⊥x轴,垂足为B,顶点C在第四象限,△ABC的中线BD交y轴于点E,连接CE,若△BCE的面积是6,则k的值为-12.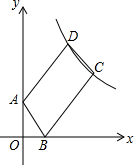 如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.