题目内容
8.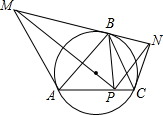 锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.
锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.
分析 过M作MD⊥AC于D,过N作NE⊥AC于E,由MN是⊙O的切线,根据弦切角定理等等∠NAB=∠ACB,∠NCB=∠CAB,于是得到∠MAC=∠NCA,∠DAM=∠ECN,推出△ADM∽△CEN,得到$\frac{MD}{NE}=\frac{DP}{EP}$,由MD∥BP∥NE,得到$\frac{MB}{NB}=\frac{DP}{EP}$,由于MA,NC分别是⊙O的切线,得到AM=BM,CN=BN,于是得到$\frac{MD}{NE}=\frac{MA}{NC}=\frac{MB}{NB}=\frac{DP}{EP}$,证得Rt△DMP∽Rt△ENP,即可得出结论.
解答  证明:过M作MD⊥AC于D,过N作NE⊥AC于E,
证明:过M作MD⊥AC于D,过N作NE⊥AC于E,
∵MN是⊙O的切线,
∴∠NAB=∠ACB,∠NCB=∠CAB,
∴∠MAC=∠NCA,∠DAM=∠ECN,
∴△ADM∽△CEN,
∴$\frac{MD}{NE}=\frac{DP}{EP}$,
∵MD⊥AC,NE⊥AC,BP⊥AC,
∴MD∥BP∥NE,
∴$\frac{MB}{NB}=\frac{DP}{EP}$,
∵MA,NC分别是⊙O的切线,
∴AM=BM,CN=BN,
∴$\frac{MD}{NE}=\frac{MA}{NC}=\frac{MB}{NB}=\frac{DP}{EP}$,
∴Rt△DMP∽Rt△ENP,
∴∠DPM=EPN,
∴∠MPB=∠NPB.
点评 本题考查了切线的性质,相似三角形的判定和性质,弦切角定理,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
3.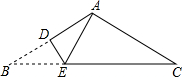 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
17.顺次连接一个四边形各边的中点,得到一个矩形,则原四边形一定是( )
| A. | 菱形 | B. | 矩形 | ||
| C. | 对角线相等的四边形 | D. | 对角线垂直的四边形 |
 如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,过点O画直线EF分别交AD,BC于点E,F,求证:AE=CF.
如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,过点O画直线EF分别交AD,BC于点E,F,求证:AE=CF. 如图,菱形ABCD的边长为8,∠C=60°,E为CD中点,作∠AEG=60°,交BC于点F,交AB的延长线于点G,则线段BG的长为$\frac{4}{3}$.
如图,菱形ABCD的边长为8,∠C=60°,E为CD中点,作∠AEG=60°,交BC于点F,交AB的延长线于点G,则线段BG的长为$\frac{4}{3}$.