题目内容
20．计算：（1$\frac{7}{2007}$+3$\frac{7}{669}$+9$\frac{7}{223}$）÷（1$\frac{1}{2007}$+3$\frac{1}{669}$+9$\frac{1}{223}$）．分析 先把带分数化为假分数，提出分子，再相除求解即可．
解答 解：（1$\frac{7}{2007}$+3$\frac{7}{669}$+9$\frac{7}{223}$）÷（1$\frac{1}{2007}$+3$\frac{1}{669}$+9$\frac{1}{223}$）
=[2014×（$\frac{1}{2007}$+$\frac{1}{669}$+$\frac{1}{223}$）]÷[2008×（$\frac{1}{2007}$+$\frac{1}{669}$+$\frac{1}{223}$）]，
=$\frac{2014}{2008}$，
=$\frac{1007}{1004}$．
点评 本题主要考查了有理数的混合运算，解题的关键是把带分数化为假分数，提出分子．
练习册系列答案
相关题目
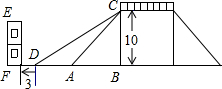如图是成都市某街道的一座人行天桥的示意图，天桥的高是10米，坡面AC的倾斜角为45°，为了方便行人安全过天桥，市政部门决定降低坡度，使新坡面DC的倾斜角为30°，若新坡脚前需留3米的人行道，问高原坡脚10米的建筑物EF是否需要拆除？请说明理由．（参考数据：$\sqrt{3}≈1.732$，$\sqrt{2}≈1.414$．）
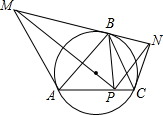锐角△ABC内接于圆，过点A和点C引外接圆的切线，它们分别交过点B的切线于M，N，而BP是△ABC 边AC上的高（P为垂足），求证：∠MPB=∠NPB．
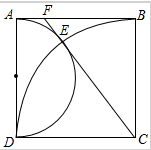如图，在边长为4的正方形ABCD中，以AD为直径的⊙O，以C为圆心的圆弧BD，与⊙O交于点E，连接CE，并延长交AB于点F．
9．若（x+8）（x-4）=x2+px+q，那么p，q的值为（ ）
| A． | 4，32 | B． | 4，-32 | C． | -4，32 | D． | -4，-32 |
如图表示a、b、c在数轴上的位置，请化简|a+b|+|c-b|+|b-a|=-3b+c．