题目内容
3.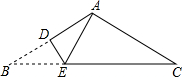 如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )
如图,△ABC是一张顶角为120°的三角形纸片,AB=AC,BC=12,现将△ABC折叠,使点B与点A 重合,折痕为DE,则DE的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3 |
分析 根据折叠的性质,AE=BE,∠DAE=∠B=30°,又∠BAC=120°,可知∠EAC=90°,根据30°所对的直角边等于斜边的一半,可知AE=4,DE=2.
解答 解:∵∠BAC=120°,
∴∠B=∠C=30°,
根据折叠的性质,AE=BE,∠DAE=∠B=30°,
∴∠EAC=90°,
∴AE=$\frac{1}{2}$EC,
∵BC=12,
∴AE=4,
∵∠ADE=90°,∠DAE=30°,
∴DE=2.
故选:B.
点评 本题主要考查了折叠的性质、等腰三角形的性质以及30°所对的直角边等于斜边的一半,熟悉折叠的性质是解决问题的关键.

练习册系列答案
相关题目
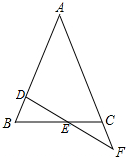 如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗?
如图,在△ABC中,AB=AC,直线DF交AB于点D,交AC的延长线于点F,交BC于点E,若BD=CF,你能证明E是DF的中点吗? 如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.
如图,AB<BC,AD=DC,∠ABD=∠DBC,说明∠A+∠C=180°.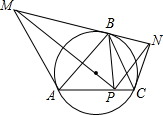 锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.
锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.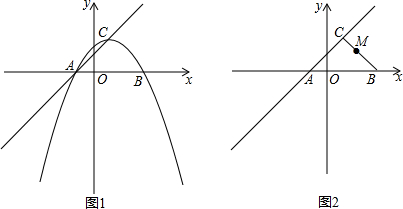
 如图,在平行四边形ABCD中,E、F分别是边BC、AD的中点,连接DE、BF,求证:四边形BEDF是平行四边形.
如图,在平行四边形ABCD中,E、F分别是边BC、AD的中点,连接DE、BF,求证:四边形BEDF是平行四边形.