题目内容
18. 如图,菱形ABCD的边长为8,∠C=60°,E为CD中点,作∠AEG=60°,交BC于点F,交AB的延长线于点G,则线段BG的长为$\frac{4}{3}$.
如图,菱形ABCD的边长为8,∠C=60°,E为CD中点,作∠AEG=60°,交BC于点F,交AB的延长线于点G,则线段BG的长为$\frac{4}{3}$.
分析 连结BD交AE于H,利用菱形的性质,得到△ABH∽△DEH,得到DH=$\frac{1}{3}BD$,根据∠C=60°,CD=BC,所以△BCD为等边三角形,所以DH=$\frac{8}{3}$,再证明△DEH∽△CFE,求出CF=6,BF=8-6=2,由AB∥CD,△BGF∽△CFE,得到$\frac{BG}{BF}=\frac{EC}{CF}$,即$\frac{BG}{2}=\frac{4}{6}$,所以BG=$\frac{4}{3}$.
解答 解:如图,连BD交AE于H,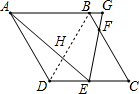
∵四边形ABCD为菱形,
∴AB∥CD,
∴△ABH∽△DEH,
∴$\frac{DH}{BH}=\frac{DE}{AB}$
即$\frac{DH}{BH}=\frac{4}{8}=\frac{1}{2}$
∴DH=$\frac{1}{2}$BH,
∴DH=$\frac{1}{3}BD$,
∵∠C=60°,CD=BC,
∴△BCD为等边三角形,
∴BD=CD=BC=8,∠BDC=∠C=60°,
∴DH=$\frac{8}{3}$,
∵∠DEH+∠AEG+∠FEC=180°,
∠CFE+∠C+∠FEC=180°,∠AEG=∠C=60°,
∴∠DEH=∠CFE,
在△DEH和△CFE中,
$\left\{\begin{array}{l}{∠BDC=∠C}\\{∠DEH=∠CFE}\end{array}\right.$,
∴△DEH∽△CFE,
∴$\frac{DH}{DE}=\frac{EC}{CF}$
即$\frac{\frac{8}{3}}{4}=\frac{4}{CF}$
∴CF=6,
即BF=8-6=2,
∵AB∥CD,
∴△BGF∽△CFE,
∴$\frac{BG}{BF}=\frac{EC}{CF}$,
即$\frac{BG}{2}=\frac{4}{6}$,
∴BG=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查了菱形的性质、相似三角形的性质定理和判定定理,解决本题的关键是证明三角形相似.

 阅读快车系列答案
阅读快车系列答案| A. | 4,32 | B. | 4,-32 | C. | -4,32 | D. | -4,-32 |
| A. | $\frac{1.5×200}{x}$-$\frac{240}{x}$=4 | B. | $\frac{240}{1.5x}$-$\frac{200}{4}$=4 | ||
| C. | $\frac{200}{x}$-$\frac{240}{1.5x}$=4 | D. | $\frac{1.5x+200}{x+4}$=$\frac{240}{x}$ |
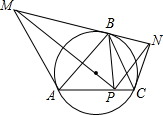 锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.
锐角△ABC内接于圆,过点A和点C引外接圆的切线,它们分别交过点B的切线于M,N,而BP是△ABC 边AC上的高(P为垂足),求证:∠MPB=∠NPB.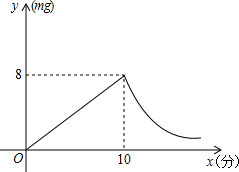 为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题: 如图,在平行四边形ABCD中,E、F分别是边BC、AD的中点,连接DE、BF,求证:四边形BEDF是平行四边形.
如图,在平行四边形ABCD中,E、F分别是边BC、AD的中点,连接DE、BF,求证:四边形BEDF是平行四边形. 如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点. 如图表示a、b、c在数轴上的位置,请化简|a+b|+|c-b|+|b-a|=-3b+c.
如图表示a、b、c在数轴上的位置,请化简|a+b|+|c-b|+|b-a|=-3b+c.