题目内容
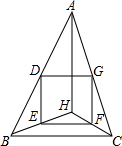 如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.
如图,锐角△ABC中,点H是三条高的交点,点D、E、F、G分别是AB、BH、CH、AC的中点.(1)求证:四边形DEFG是矩形;
(2)若∠BAC=45°,求证:四边形DEFG是正方形.
考点:中点四边形
专题:证明题
分析:(1)利用中位线的性质与判定结合平行四边形的判定得出四边形DEFG是平行四边形,进而得出∠EDG=90°,求出即可;
(2)利用全等三角形的判定得出△DME≌△FHE(ASA),进而得出DE=EF,即可得出四边形DEFG是正方形.
(2)利用全等三角形的判定得出△DME≌△FHE(ASA),进而得出DE=EF,即可得出四边形DEFG是正方形.
解答: 证明:(1)∵锐角△ABC中,点D、E、F、G分别是AB、BH、CH、AC的中点,
证明:(1)∵锐角△ABC中,点D、E、F、G分别是AB、BH、CH、AC的中点,
∴DG∥BC,DE∥AH,FG∥AH,EF∥BC,
∴DG∥EF,DE∥FG,
∴四边形DEFG是平行四边形,
∵点H是三条高的交点,DG∥BC,
∴AH⊥DG,
∴∠EDG=90°,
∴平行四边形DEFG是矩形;
(2)延长CH交AB于M,延长BH交AC于N,
∵点H是三条高的交点,
∴∠AMH=90°,
∵∠BAC=45°,
∴∠MHN=360°-90°-90°-45°=135°,
∴∠1=135°,
∴∠MHB=45°,
∴∠MBH=45°,
∴BM=MH,
∵BE=EH,
∴ME⊥BH,
∴ME=EH,则∠EMH=45°,
∴∠EMD=135°,
则∠EMD=∠EHF,
∵∠FEH+∠DEH=90°,∠DEH+∠DEM=90°,
∴∠DEM=∠FEH,
在△DME和△FHE中
∵
,
∴△DME≌△FHE(ASA),
∴DE=EF,
∴矩形DEFG是正方形.
 证明:(1)∵锐角△ABC中,点D、E、F、G分别是AB、BH、CH、AC的中点,
证明:(1)∵锐角△ABC中,点D、E、F、G分别是AB、BH、CH、AC的中点,∴DG∥BC,DE∥AH,FG∥AH,EF∥BC,
∴DG∥EF,DE∥FG,
∴四边形DEFG是平行四边形,
∵点H是三条高的交点,DG∥BC,
∴AH⊥DG,
∴∠EDG=90°,
∴平行四边形DEFG是矩形;
(2)延长CH交AB于M,延长BH交AC于N,
∵点H是三条高的交点,
∴∠AMH=90°,
∵∠BAC=45°,
∴∠MHN=360°-90°-90°-45°=135°,
∴∠1=135°,
∴∠MHB=45°,
∴∠MBH=45°,
∴BM=MH,
∵BE=EH,
∴ME⊥BH,
∴ME=EH,则∠EMH=45°,
∴∠EMD=135°,
则∠EMD=∠EHF,
∵∠FEH+∠DEH=90°,∠DEH+∠DEM=90°,
∴∠DEM=∠FEH,
在△DME和△FHE中
∵
|
∴△DME≌△FHE(ASA),
∴DE=EF,
∴矩形DEFG是正方形.
点评:此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质和矩形以及正方形的判定等知识,得出△DME≌△FHE(ASA)是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )
如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )| A、5 | B、6 | C、7 | D、8 |
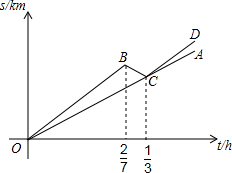 某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.
某自行车队根据队员速度的不同,分为快1组、快2组、慢1组和慢2组四个小组,在该车队的一次训练中,快1组和慢1组从甲地行进到乙地,剩下的组从乙地行进到甲地.快1组和慢1组同时从甲地出发,快1组的队员以高于慢1组队员10km/h的速度前行,快1组行驶一段时间后因某些原因又往回行驶(在往返过程中速度不变),最终与慢1组汇合,汇合后两组继续以各自的速度向乙地行进.设快1组和慢1组行驶的时间为t,与甲地的距离为s,s与t之间的函数图象如图所示.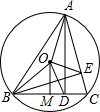 如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.
如图,锐角△ABC内接于圆O,AD⊥BC,BE⊥AC,OM⊥BC,垂足分别为D、E、M.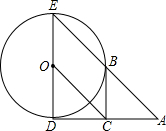 如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.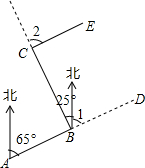 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?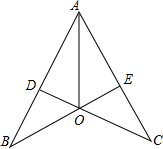 如图:AB=AC,BD=CE.求证:OA平分∠BAC.
如图:AB=AC,BD=CE.求证:OA平分∠BAC. 一只自由飞行的小鸟,将随意地落在如图所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为
一只自由飞行的小鸟,将随意地落在如图所示方格地面上(每个小方格都是边长相等的正方形),则小鸟落在阴影方格地面上的概率为