题目内容
1.如图①,已知AC是矩形纸片ABCD的对角线,AB=3,BC=4.现将矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图②中△A′BC′,当四边形A′ECF是菱形时,平移距离AA′的长是$\frac{5}{2}$.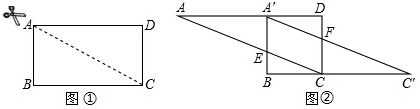
分析 由矩形的性质求得AC=5,由平移的性质得出A′B=DC=3,设AA′=x,则A′D=4-x,由菱形的性质得出A′E∥FC,A′E=EC,由平行线的性质得出△AA′E∽△ADC,由相似的性质得出$\frac{x}{4}$=$\frac{A′E}{3}$=$\frac{AE}{5}$,求出AE=$\frac{5}{4}$x,A′E=$\frac{3}{4}$x,EC=AC-AE=5-$\frac{5}{4}$x,得出$\frac{3}{4}$x=5-$\frac{5}{4}$x,求出x即可得出结果.
解答 解:∵矩形纸片ABCD,AB=3,BC=4,
∴在图②中,AD=4,A′B=DC=3,AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设AA′=x,
∴A′D=4-x,
∵四边形A′ECF是菱形
∴A′E∥FC,A′E=EC,
∴△AA′E∽△ADC,
$\frac{AA′}{AD}$=$\frac{A′E}{DC}$=$\frac{AE}{AC}$,
即:$\frac{x}{4}$=$\frac{A′E}{3}$=$\frac{AE}{5}$,
∴AE=$\frac{5}{4}$x,A′E=$\frac{3}{4}$x,
∴EC=AC-AE=5-$\frac{5}{4}$x,
∴$\frac{3}{4}$x=5-$\frac{5}{4}$x,
解得:x=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$.
点评 本题考查了矩形的性质、勾股定理、平移的性质、菱形的性质、三角形相似的判定与性质等知识;熟练掌握三角形相似的判定与性质是解决问题的关键.

练习册系列答案
相关题目
12. 张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
 张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )
张琳同学将某地2016年6月~10月的月降水量绘制成了如图所示的折线统计图,则降雨量变化最大的时间范围是( )| A. | 6~7月份 | B. | 7~8月份 | C. | 8~9月份 | D. | 9~10月份 |
9.如果直角三角形两直角边为5:12,则斜边上的高与斜边的比为( )
| A. | 60:13 | B. | 5:12 | C. | 12:13 | D. | 60:169 |
16.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
根据表格提供的信息,下列说法错误的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
| A. | 该抛物线的对称轴是直线x=-2 | |
| B. | 该抛物线与y轴的交点坐标为(0,-2.5) | |
| C. | b2-4ac=0 | |
| D. | 若点A(0.5,y1)是该抛物线上一点.则y1<-2.5 |
6.“六•一”儿童节前夕,某超市用3000元购进A、B两种童装共120件,其中A种童装每件24元,B种童装每件30元.若设购买A种童装x件,B种童装y件,依题意列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=120}\\{24x+30y=3000}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=120}\\{30x+24y=300}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{30x+24y=120}\\{x+y=3000}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{24x+30y=120}\\{x+y=3000}\end{array}\right.$ |
 (1)计算:-23+$\frac{1}{5}$(π-3)0-(-$\frac{1}{3}$)-2
(1)计算:-23+$\frac{1}{5}$(π-3)0-(-$\frac{1}{3}$)-2 如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$.
如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$.