题目内容
11. 如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$.
如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的面积为$\frac{49\sqrt{3}}{2}$.
分析 连接AC与BD相交于点O,由菱形的性质和BD长度可求出AC的长,根据菱形的面积等于对角线成绩的一半即可得到问题答案.
解答 解:
连接AC与BD相交于点O,
∵四边形ABCD是菱形,
∴∠DAO=∠BAO=$\frac{1}{2}$∠DAB=30°,AC⊥BD,BO=DO,AO=CO,
∵BD=7,
∴DO=$\frac{1}{2}$BD=3.5,
∴AO=$\frac{7}{2}$$\sqrt{3}$,
∴AC=2AO=7$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{49\sqrt{3}}{2}$,
故答案为:$\frac{49\sqrt{3}}{2}$.
点评 本题考查了菱形的性质以及菱形的面积的等于对角线乘积的一半的求解方法,求出AC的长是解题的关键也是本题的突破口.

练习册系列答案
相关题目
16. 如图△ABC中∠C=90°,∠B=30°,将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角为( )
如图△ABC中∠C=90°,∠B=30°,将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角为( )
 如图△ABC中∠C=90°,∠B=30°,将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角为( )
如图△ABC中∠C=90°,∠B=30°,将△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角为( )| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
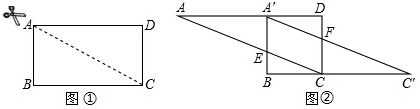
 如图,?ABCD中,对角线AC,BD相交于点O,OA=3,若要使平行四边形ABCD为矩形,则OB的长度为( )
如图,?ABCD中,对角线AC,BD相交于点O,OA=3,若要使平行四边形ABCD为矩形,则OB的长度为( )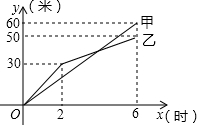 某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:
某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题: