题目内容
19.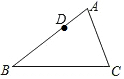 在△ABC中,AB=6,AC=4,D是线段AB上的一点,且AD=2,若E是线段AC上的一点,且△ADE与△ABC相似,则AE=$\frac{4}{3}$或3.
在△ABC中,AB=6,AC=4,D是线段AB上的一点,且AD=2,若E是线段AC上的一点,且△ADE与△ABC相似,则AE=$\frac{4}{3}$或3.
分析 根据题意,△ADE与△ABC相似,由于题中没有指明对应边,故应该分两种情况讨论求解.
解答 解:①当△ADE∽△ABC时,有$\frac{AD}{AE}=\frac{AB}{AC}$,
∵AB=6,AC=4,AD=2,
∴$\frac{2}{AE}$=$\frac{6}{4}$
∴解得:AE=$\frac{4}{3}$;
②当△AED∽△ABC时,有$\frac{AD}{AE}$=$\frac{AC}{AB}$,
∵AB=6,AC=4,AD=2,
∴$\frac{2}{AE}$=$\frac{4}{6}$,
∴解得:AE=3,
所以AE等于3或$\frac{4}{3}$.
故答案为:3或$\frac{4}{3}$.
点评 此题考查了相似三角形的性质,注意分类讨论思想的运用是解题关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
10.数轴上A、B两点位于原点O的两侧,点A表示的实数是a,点B表示的实数是b,若|a-b|=2013,且AO=2BO,则a+b的值是( )
| A. | 671 | B. | 2013 | C. | -671 | D. | ±671 |
9.某一次函数的图象经过点(-3,6),且函数值y随自变量x的增大而增大,则下列函数中符合上述条件的是( )
| A. | y=-3x-3 | B. | y=4x+6 | C. | y=-2x+12 | D. | y=x+9 |
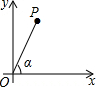 如图,在直角坐标平面内,点P与原点O的距离OP=13,OP与x轴正半轴的夹角α的余弦值为$\frac{5}{13}$,则点P的坐标是(5,12).
如图,在直角坐标平面内,点P与原点O的距离OP=13,OP与x轴正半轴的夹角α的余弦值为$\frac{5}{13}$,则点P的坐标是(5,12). 小明在写作业时不甚将一滴钢笔水滴在数轴上,根据图中的数值,判断被墨迹盖住的整数有-2,-1,0,2,3.
小明在写作业时不甚将一滴钢笔水滴在数轴上,根据图中的数值,判断被墨迹盖住的整数有-2,-1,0,2,3.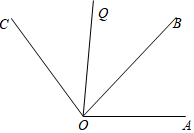 如图,OQ是∠BOC的平分线,
如图,OQ是∠BOC的平分线,