题目内容
4.三月份学校开展了“朗读月”系列活动,活动结束后,为了表彰优秀,学校准备购买一些钢笔和笔记本作为奖品进行奖励,如果购买3支钢笔和4本笔记本需要93元;如果买2支钢笔和5本笔记本需要90元.(1)试求出每支钢笔和每本笔记本的价格是多少元?
(2)学校计划用不超过500元购买两种奖品共40份,问:最多可以买几支钢笔?
分析 (1)首先用未知数设出买一支钢笔和一本笔记本所需的费用,然后根据关键语“购买3支钢笔和4本笔记本需要93元;买2支钢笔和5本笔记本需要90元”,列方程组求出未知数的值,即可得解.
(2)设购买钢笔的数量为x,则笔记本的数量为40-x,根据总费用不超过500元,列出不等式解答即可.
解答 解:(1)设一支钢笔需x元,一本笔记本需y元,
由题意得:$\left\{\begin{array}{l}{3x+4y=93}\\{2x+5y=90}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=15}\\{y=12}\end{array}\right.$,
答:一支钢笔需15元,一本笔记本需12元.
(2)设购买钢笔的数量为x,则笔记本的数量为(40-x)本,
由题意得:15x+12(40-x)≤500,
解得:x≤6$\frac{2}{3}$,
答:学校最多可以购买6支钢笔.
点评 此题主要考查了二元一次方程组和一元一次不等式的应用,关键是正确理解题意,找出等量关系,列出方程组和不等式.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
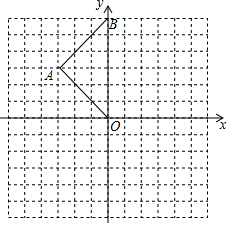 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△OAB的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△OAB的顶点均在格点上.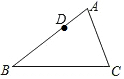 在△ABC中,AB=6,AC=4,D是线段AB上的一点,且AD=2,若E是线段AC上的一点,且△ADE与△ABC相似,则AE=$\frac{4}{3}$或3.
在△ABC中,AB=6,AC=4,D是线段AB上的一点,且AD=2,若E是线段AC上的一点,且△ADE与△ABC相似,则AE=$\frac{4}{3}$或3. 解不等式组:$\left\{\begin{array}{l}{x-3≤0,①}\\{\frac{3x+1}{12}<\frac{2x-1}{3}.②}\end{array}\right.$并把不等式组的解集表示在数轴上.
解不等式组:$\left\{\begin{array}{l}{x-3≤0,①}\\{\frac{3x+1}{12}<\frac{2x-1}{3}.②}\end{array}\right.$并把不等式组的解集表示在数轴上. 如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.
如图所示,在△ABC中,∠A=70°,点D是BC延长线上的一点,∠ACD=150°,则∠B=80°.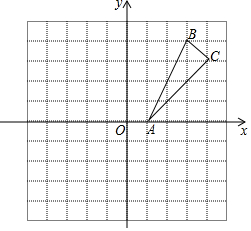 如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上;
如图,在平面直角坐标系中,每一格表示1个单位长度,△ABC的三个顶点都在格点上;